Population Ecology, part 3

Principles of Ecology Week 4

Exponential and stage-structured population growth

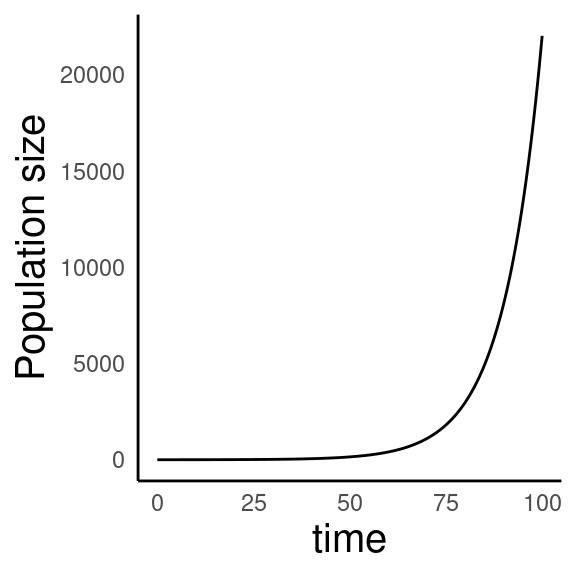
Exponential growth

\[\frac{dN}{dt} = rN\]

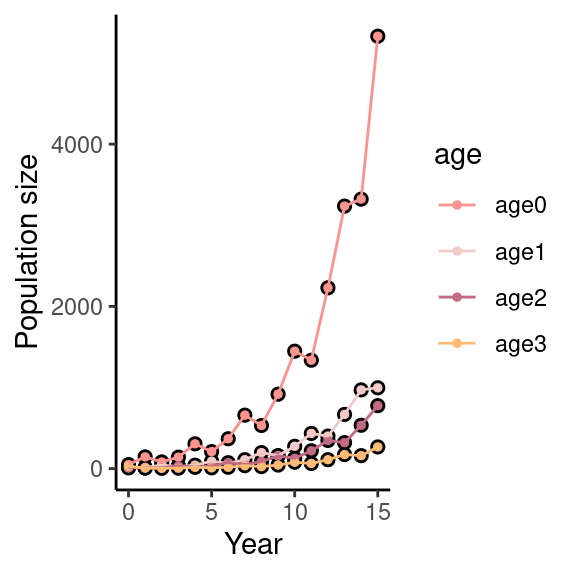
Stage-structured growth

\[N_{t+1} = \text{[transition matrix]} ~x~ \\ \text{[population vector]}\]

Exponential and stage-structured population growth

Exponential growth

\[\frac{dN}{dt} = rN\]

Stage-structured growth

\[N_{t+1} = \text{[transition matrix]} ~x~ \\ \text{[population vector]}\]

When is population at equilibrium??

(But first, what is “Equilibrium” in ecology?)

In ecological systems, “equilibrium” means no change in population size (or other relevant aspect of a system) over time

Under exponential population is at equilibrium only when \(N = 0\)

Populations with \(r = 0\) or \(\lambda = 1\) are also at equilibrium (no net births or deaths)

Key assumptions of the exponential growth model

• No immigration or emigration (Closed population)

• Constant birth and death rate (\(b\) and \(d\) don’t vary with \(N\))

• No variation within population (all individuals have similar \(b\) and \(d\)) (This implies that \(b\) and \(d\) don’t vary with age or stage)

• Continuous population growth without time lags
  (e.g. no seasonality)

Key assumptions of the exponential growth model

• No immigration or emigration (Closed population)

• Constant birth and death rate (\(b\) and \(d\) don’t vary with \(N\))

• No variation within population (all individuals have similar \(b\) and \(d\)) (This implies that \(b\) and \(d\) don’t vary with age or stage)
  We relaxed this for stage-structured growth

• Continuous population growth without time lags
  (e.g. no seasonality)

Key assumptions of the exponential growth model

• No immigration or emigration (Closed population)

• Constant birth and death rate (\(b\) and \(d\) don’t vary with \(N\))
  What if we relax this assumption? –> Density-dependent growth

• No variation within population (all individuals have similar \(b\) and \(d\)) (This implies that \(b\) and \(d\) don’t vary with age or stage)

• Continuous population growth without time lags
  (e.g. no seasonality)

Constant birth and death rate (\(b\) and \(d\) don’t vary with \(N\))

Constant birth and death rate (\(b\) and \(d\) don’t vary with \(N\))

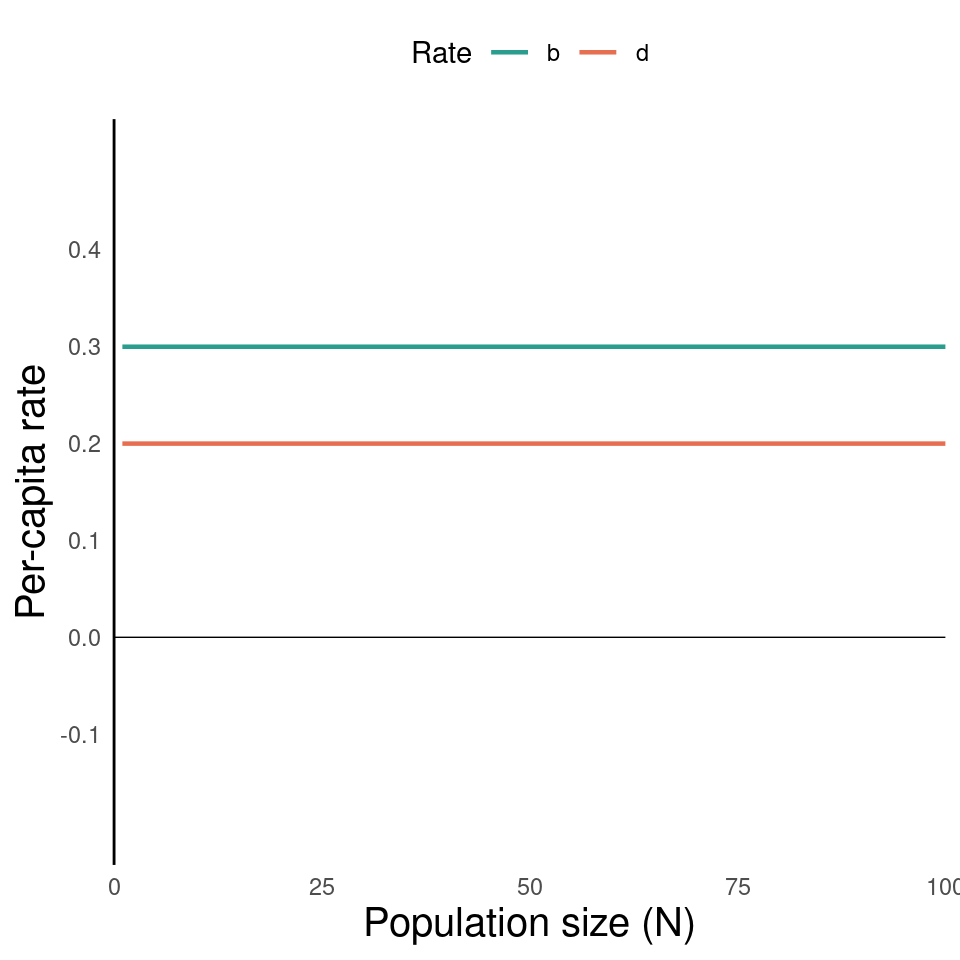
Constant birth and death rate (\(b\) and \(d\) don’t vary with \(N\))

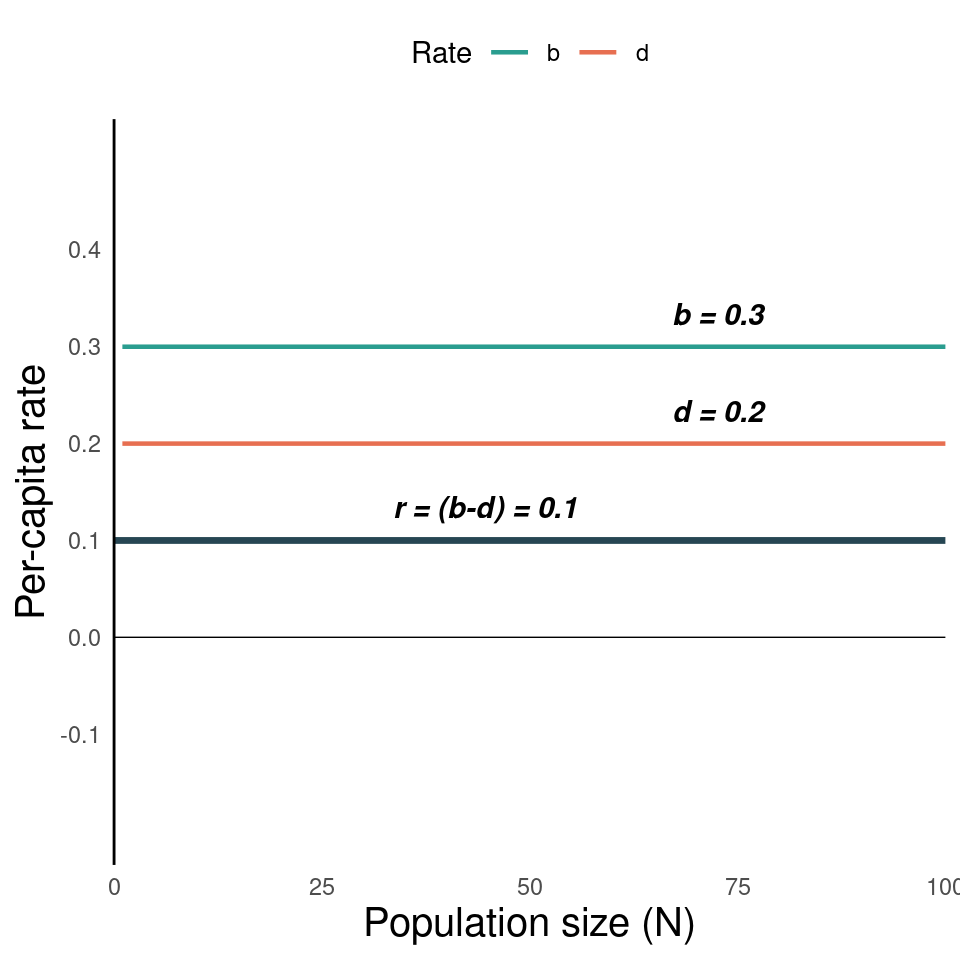
What if \(b\) and \(d\) are not constant?

We can easily imagine scenarios in which birth and death rates vary with population size.

• In social species (bees, ants, wolves, some woodpeckers, etc.), birth rates (\(b\)) might increase with population size

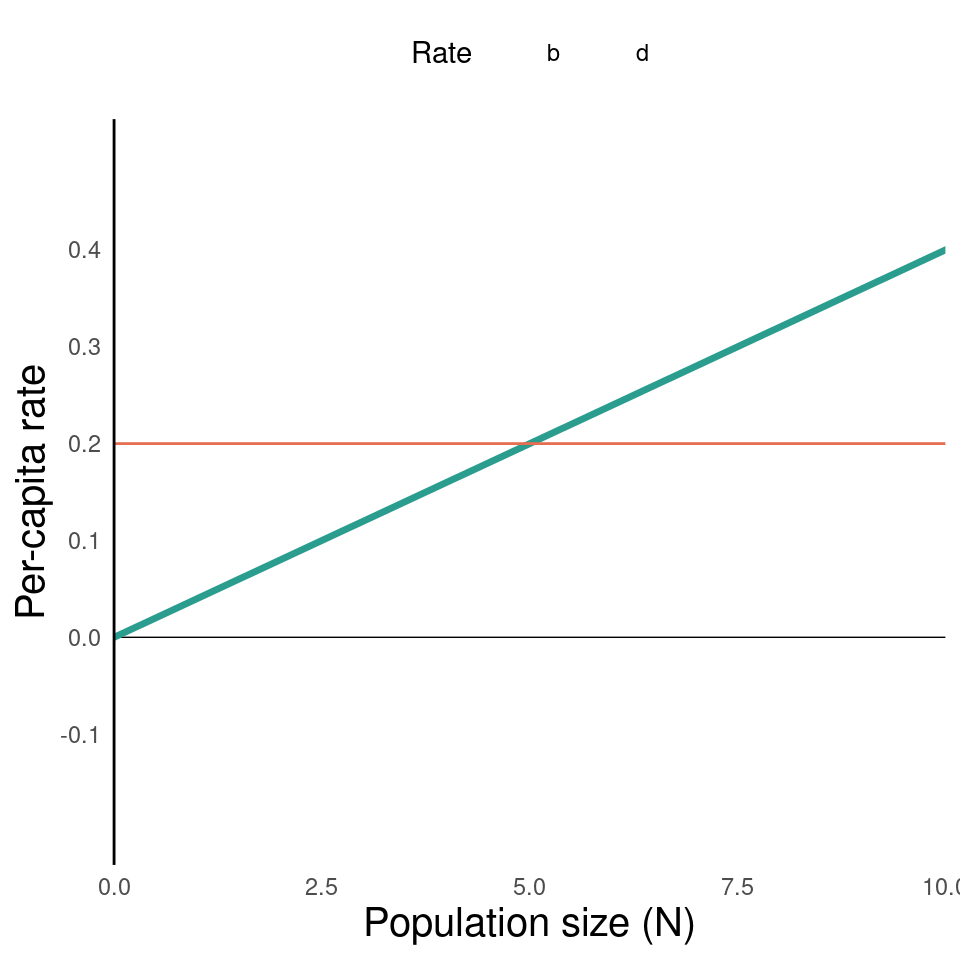
What if \(b\) and \(d\) are not constant?

We can easily imagine scenarios in which birth and death rates vary with population size.

• Under strict resource limitation, mortality rate might increase with population size
  • Could also happen without resource limitation, e.g. higher rates of disease spread

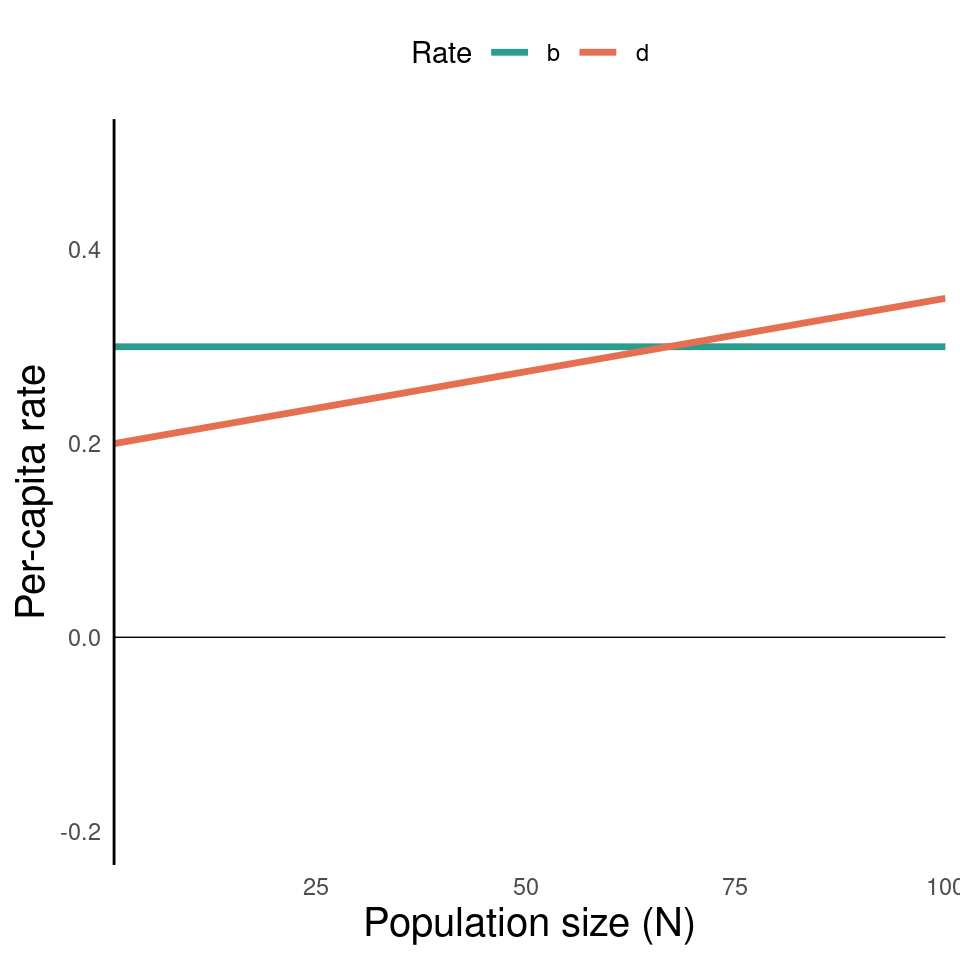
• Under this assumption (\(d\) increases with \(N\)), we see that there is a point at which \(\text{growth rate} = 0\).

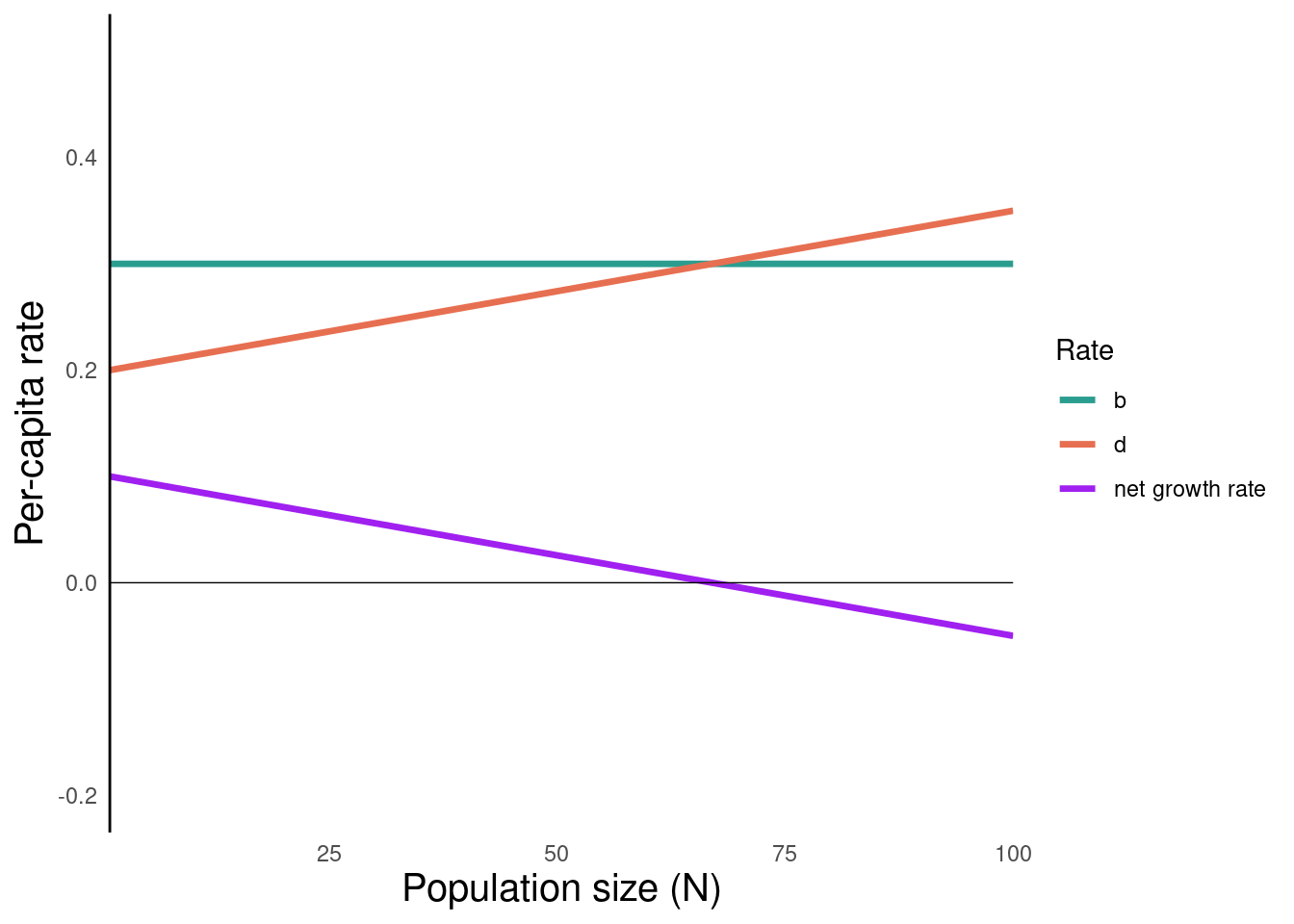
• \(r\) is the growth rate when \(N = 0\)

What happens when \(b-d = 0\)?

• Birth rate equals death rate
• No change in population size
  population is at an equilibrium

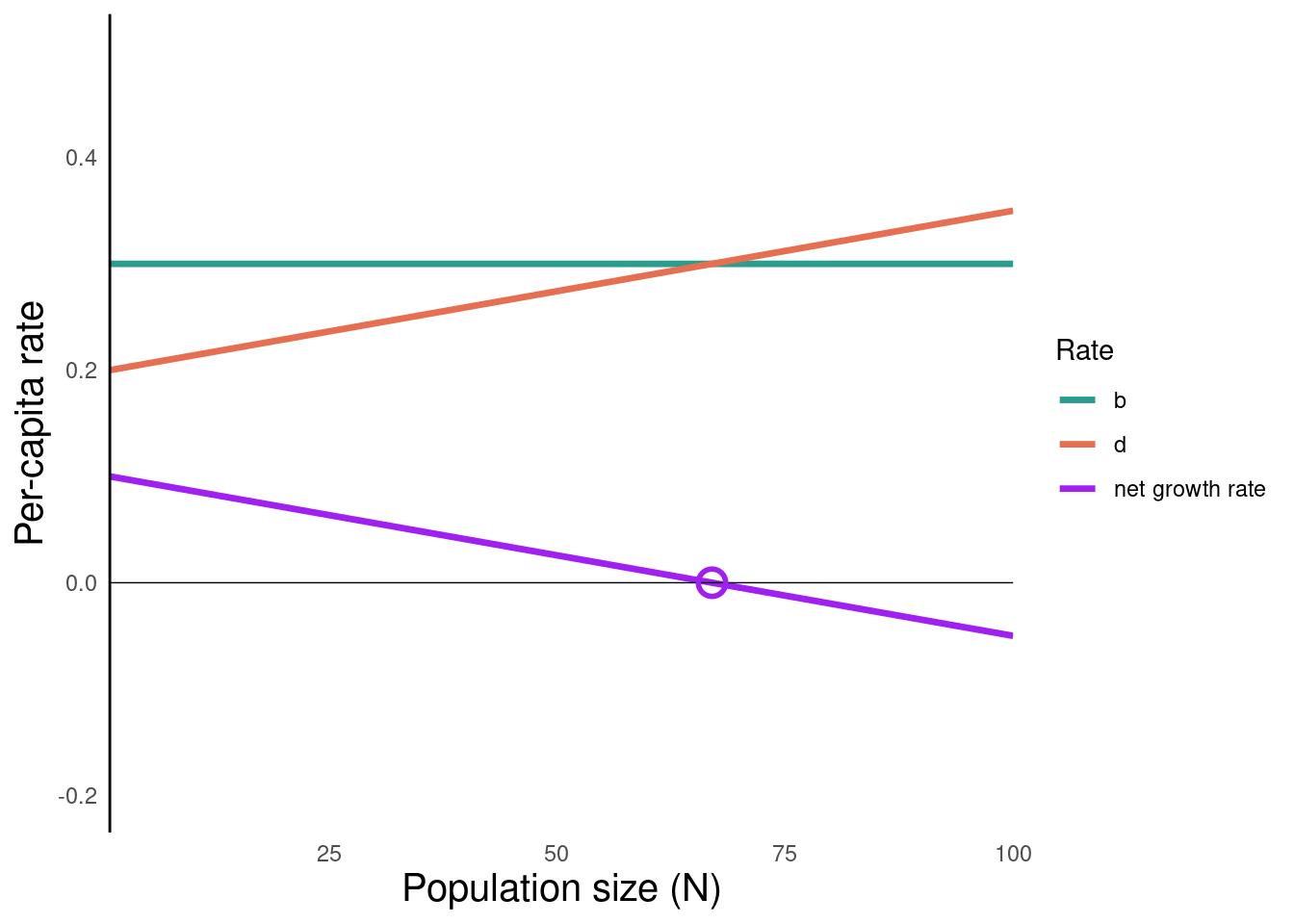
• The population size (\(N\)) at which growth rate equals zero is called the carrying capacity (\(K\))

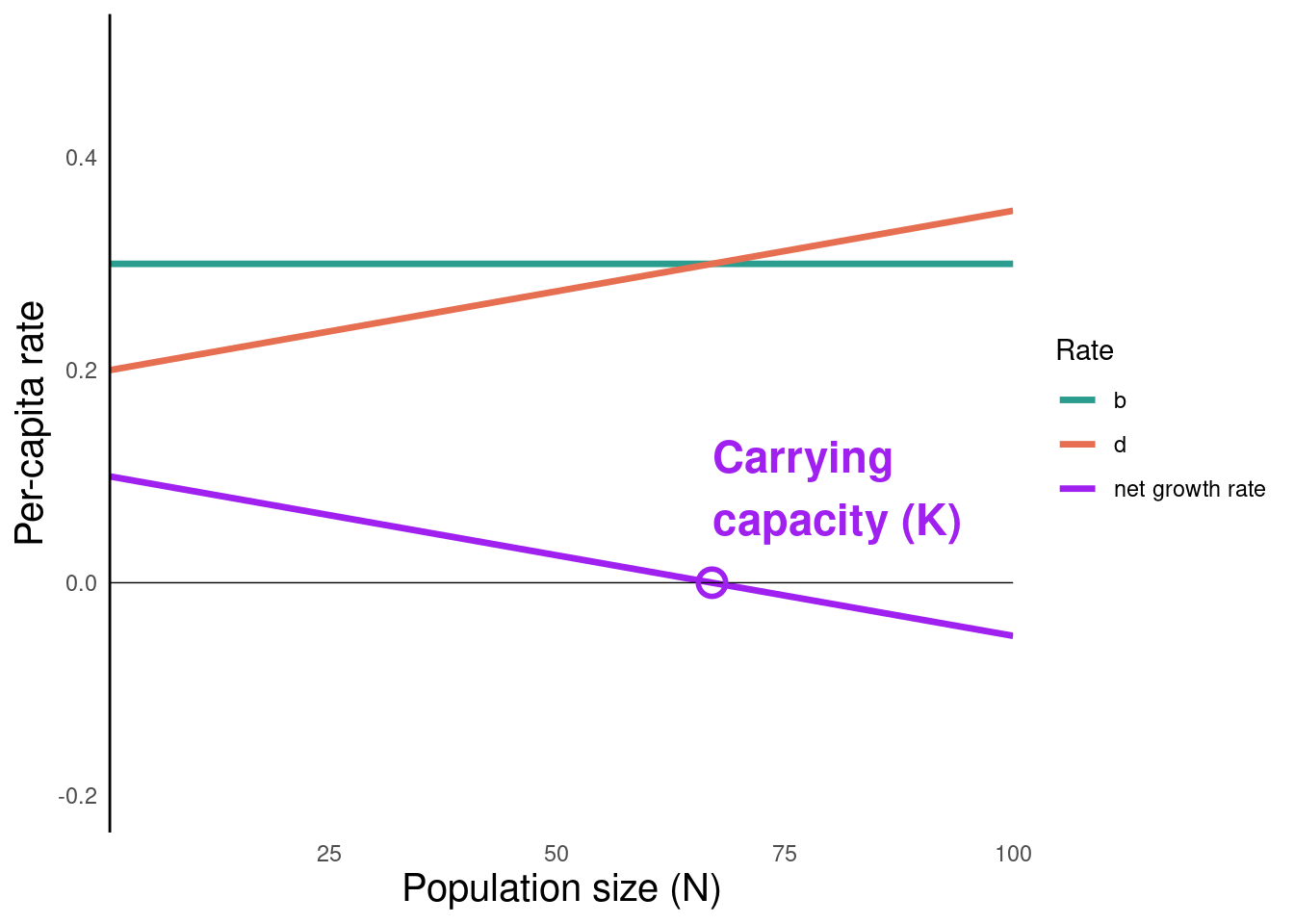
• The population size (\(N\)) at which growth rate equals zero is called the carrying capacity (\(K\))

• The population’s growth rate at \(N = 0\) is \(r\)

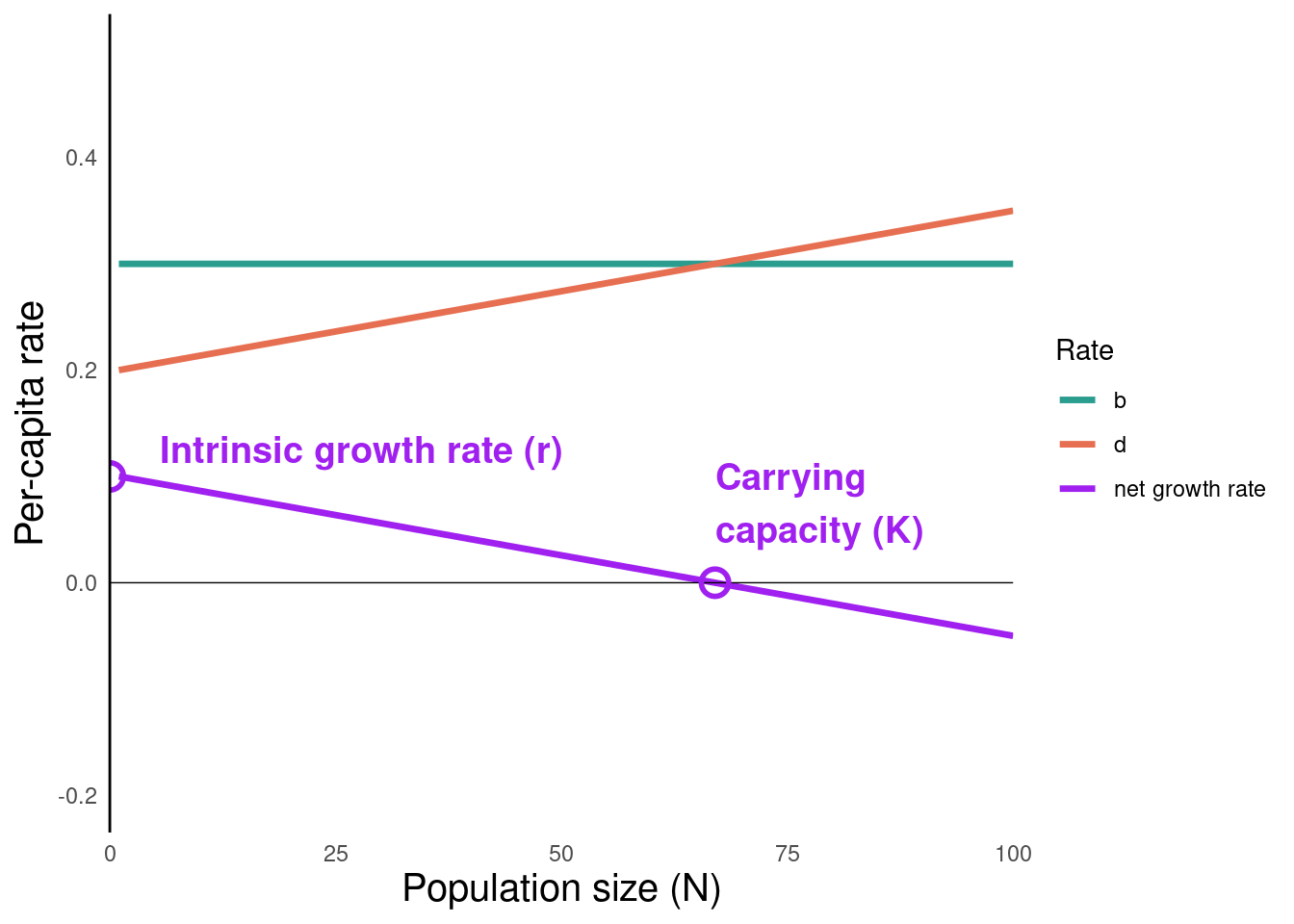
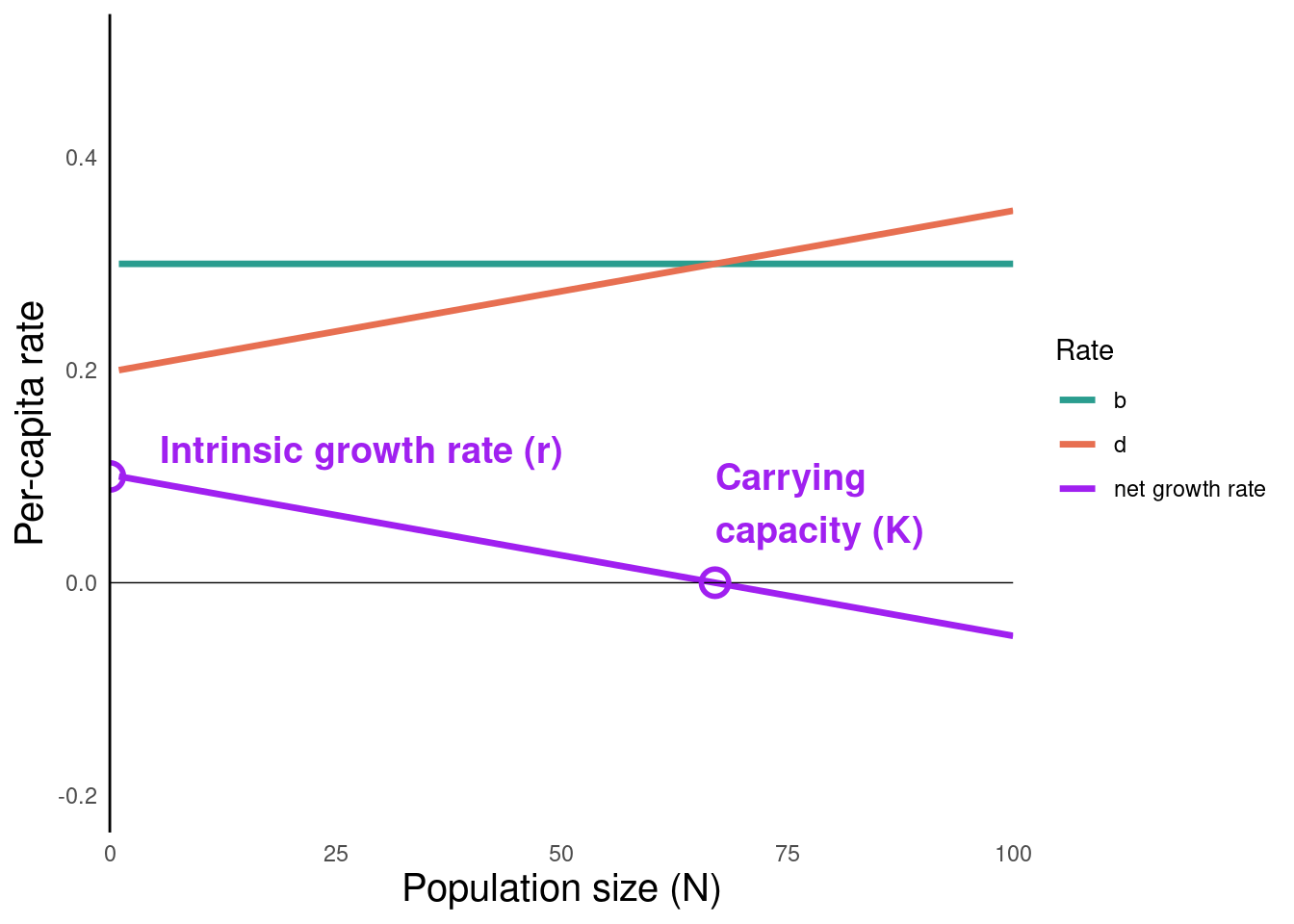
• The per-capita population growth rate (\(\frac{1}{N}\frac{dN}{dt}\)) for a population of a given size is the Y-axis value.
  • The closer a population is to \(N = 0\), the closer its actual growth rate is to \(r\)
  • The closer a population is to \(N = K\), the closer its actual growth rate is to \(0\)
    
  • Populations that are bigger than K have negative population growth (until they fall back to carrying capacity)

Mathematical expression

What is the equation of the purple line?

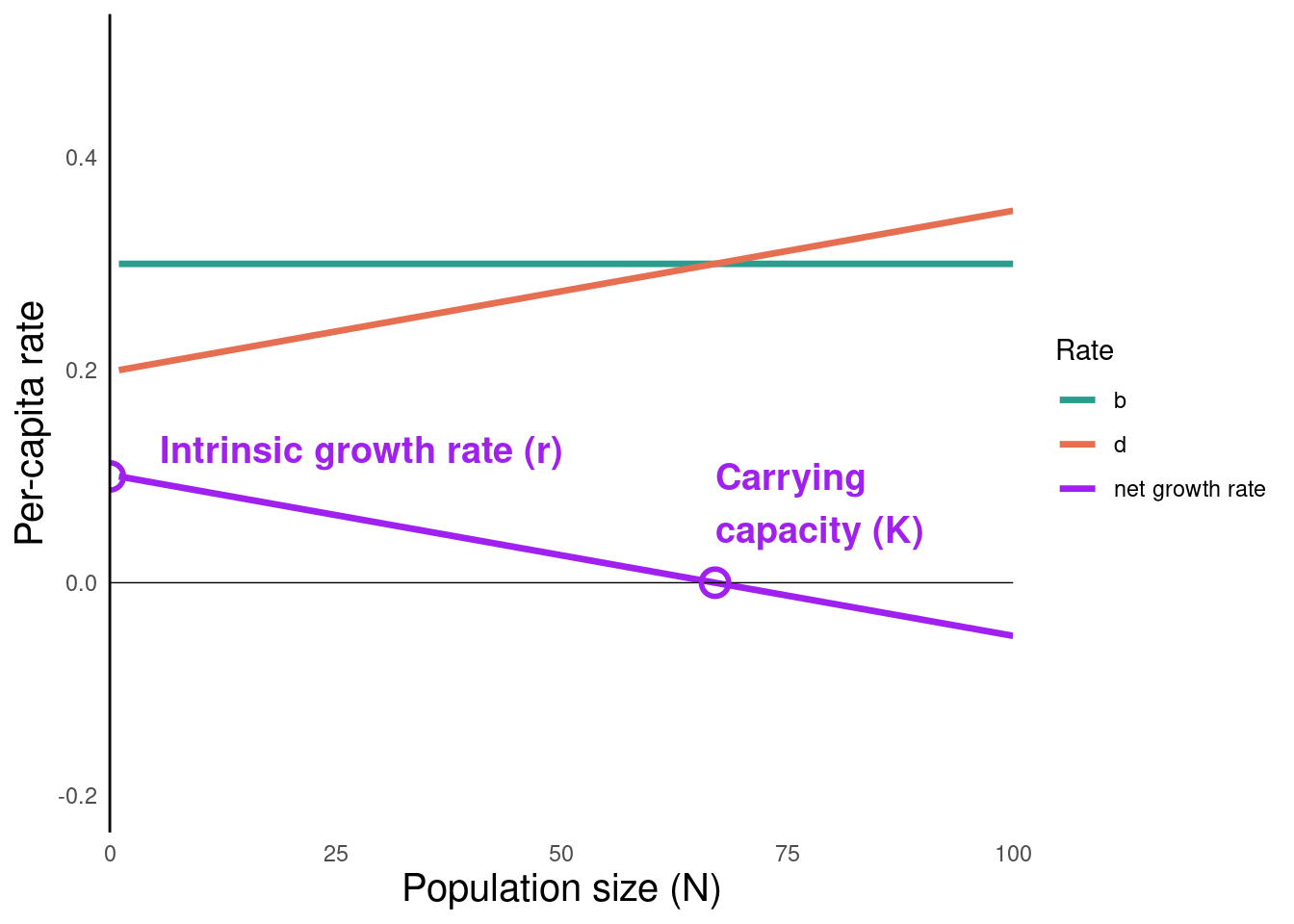
• Recall from algebra that we can use the “point-slope” approach for the slope of a line (\(y-y_1 = m(x - x_1)\))
• We know two points: \((0,r)\) and \((K,0)\)
• The slope of the line turns out to be \(-\frac{r}{K}\), which we write as \(\alpha\)
• And \(y\) gives the per-capita population growth rate \(\frac{1}{N}\frac{dN}{dt}\)

Mathematical expression

What is the equation of the purple line?

• So, we can express the line as \[\frac{1}{N}\frac{dN}{dt} = r - \alpha N\]

• Through rearranging, we get back to the equation for “realized” population growth rate (not per-capita): \[\frac{dN}{dT} = (r - \alpha N)N\]

• This is equivalent to \[\frac{dN}{dT} = rN(1-\alpha N)\]

• On your own: Convince yourself through algebra that this is equal to the canonical form of the equation: \[\frac{dN}{dt} = rN \bigg(1-\frac{N}{K}\bigg)\]

\[\frac{dN}{dt} = rN \bigg(1-\frac{N}{K}\bigg)\]

• When population size is very small (\(N \to 0\)), \(\frac{N}{K} \to 0\), and the population grows ‘exponentially’
• When population size is close to carrying capacity (\(N \to K\)), \(\frac{N}{K} \to 1\), and the population remains constant
• When population size exceeds carrying capacity (\(N > K\)), \(\frac{N}{K} > 1\), and the population growth rate is negative (shrinks)
• “Logistic growth” model

Population growth over time

Population growth over time

• Not only is the carrying capacity an equilibrium, it is a stable equilibrium
• No matter where the population starts, it will reach \(K\) and stay at \(K\) until disturbed

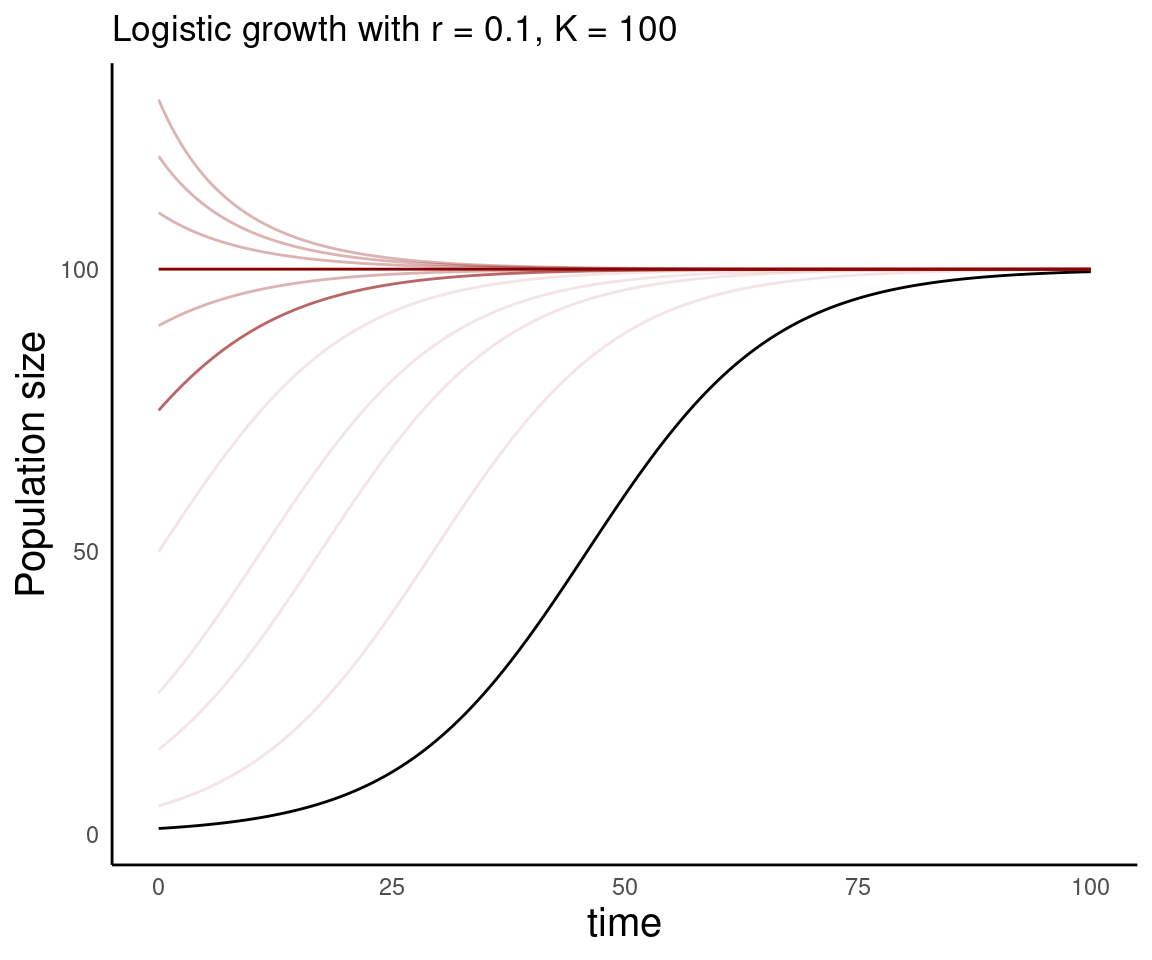
Logistic growth in nature

• The exponential growth model predicts unbounded population growth (no equlibrium)
• The logistic growth model relaxes one assumption (birth/death rates that change with \(N\))
• Now allows population sizes to saturate at a carrying capacity
  • Biological realism, but also more parameters to estimate

Population Ecology
Density-dependent population growth

Density-dependence in nature

For this fish, why might population density affect birth or death rates?

Density-dependence in models

Exponential growth

\[\frac{dN}{dt} = rN\]

Logistic growth growth

\[\frac{dN}{dt} = rN\bigg(1-\frac{N}{K}\bigg)\]

Density-dependence in models

Exponential growth

\[\frac{dN}{dt} = rN\]

\[\frac{1}{N}\frac{dN}{dt} = r\]

Logistic growth growth

\[\frac{dN}{dt} = rN\bigg(1-\frac{N}{K}\bigg)\]

\[\frac{1}{N}\frac{dN}{dt} = r\bigg(1-\frac{N}{K}\bigg)\]

Density-dependent population growth, Day 3

Reminders

• Self reflection and Semester Project assignment (potential focal communities) due Sunday night on Moodle

Plotting population dynamics

Recall from Monday

• If birth or death rates are dependent on N, so too does population growth rate

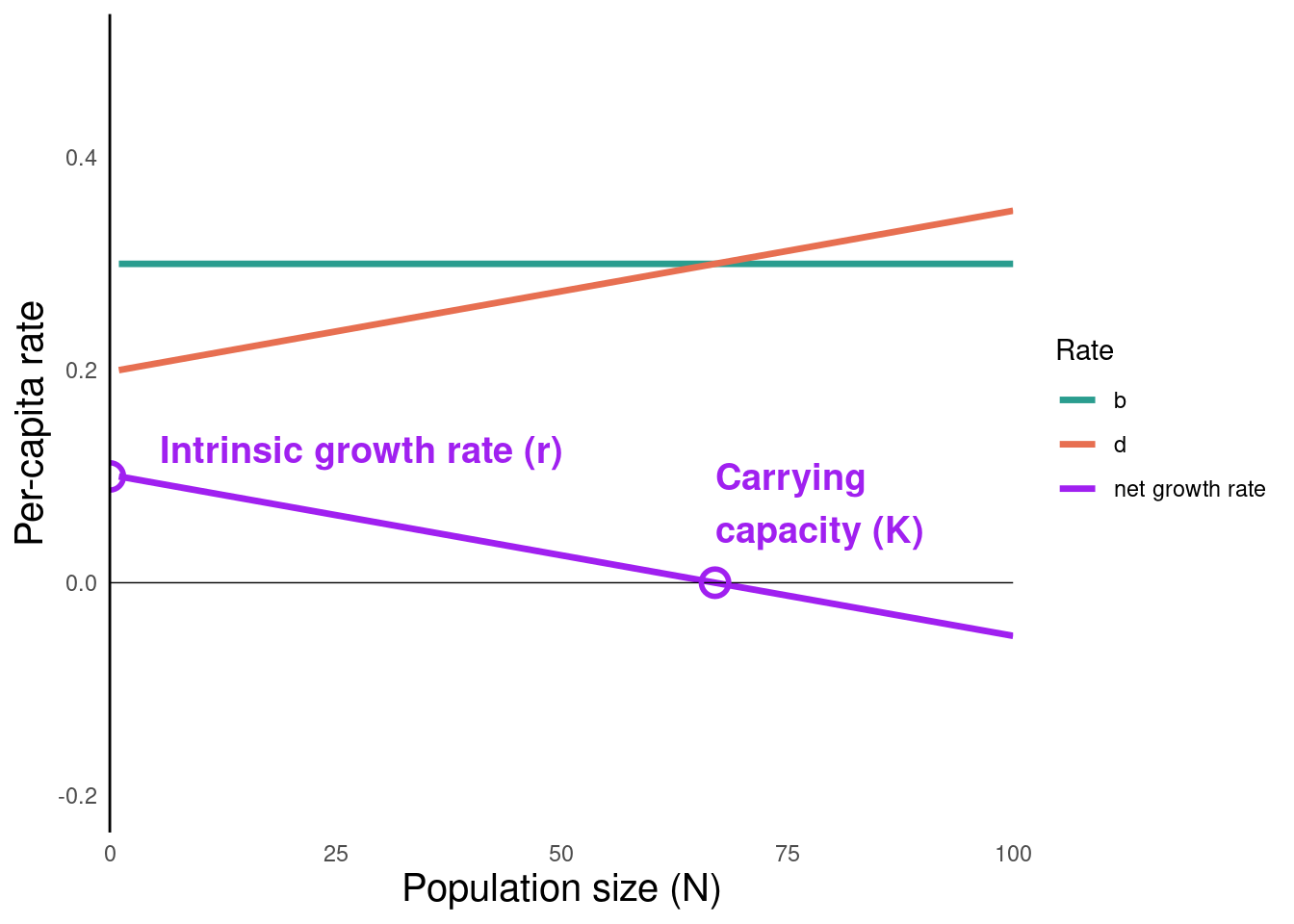
Summary of logistic growth

\[\frac{dN}{dt} = rN \bigg(1-\frac{N}{K}\bigg)\]

• When population size is very small (\(N \to 0\)), \(\frac{N}{K} \to 0\), and the population grows ‘exponentially’
• When population size is close to carrying capacity (\(N \to K\)), \(\frac{N}{K} \to 1\), and the population remains constant
• When population size exceeds carrying capacity (\(N > K\)), \(\frac{N}{K} > 1\), and the population growth rate is negative (shrinks)

Population growth over time

What is the “equilibrium” of this system

• Intuitively, we might say that the system is at equilibrium when it is at carrying capacity (\(K\))

• What is special about this?

\[\frac{dN}{dt} = rN\bigg(1-\frac{K}{N}\bigg)\] When \(N = K\), \(\frac{dN}{dt} \to 0\).

This gets us back to the definition of equilibrium in ecological systems: no net change in the system (\(\frac{dN}{dt} = 0\))

But, what about other equilibria?

\[\boxed{\frac{dN}{dt} = rN\bigg(1-\frac{K}{N}\bigg) = 0} \text{ also happens when } N = 0\]

Thus, this system has two equilibrium points:

\[N = 0 \text{ and } N = K\]

Evaluating the stability of equilibrium points

• Just because a system is “at equilibrium” doesn’t mean it will never change

• The dynamics depend on the stability of the equilibrium

• An equilibrium is considered (locally) stable if small perturbations cause the population to return to its original state.

• Alternatively, an equilibrium is unstable if small perturbations cause the system to move away from the original state

Consider a population that is at equilibrium because \(N = 0\)

A small perturbation causes \(N = 1\) (e.g. an immigration event)

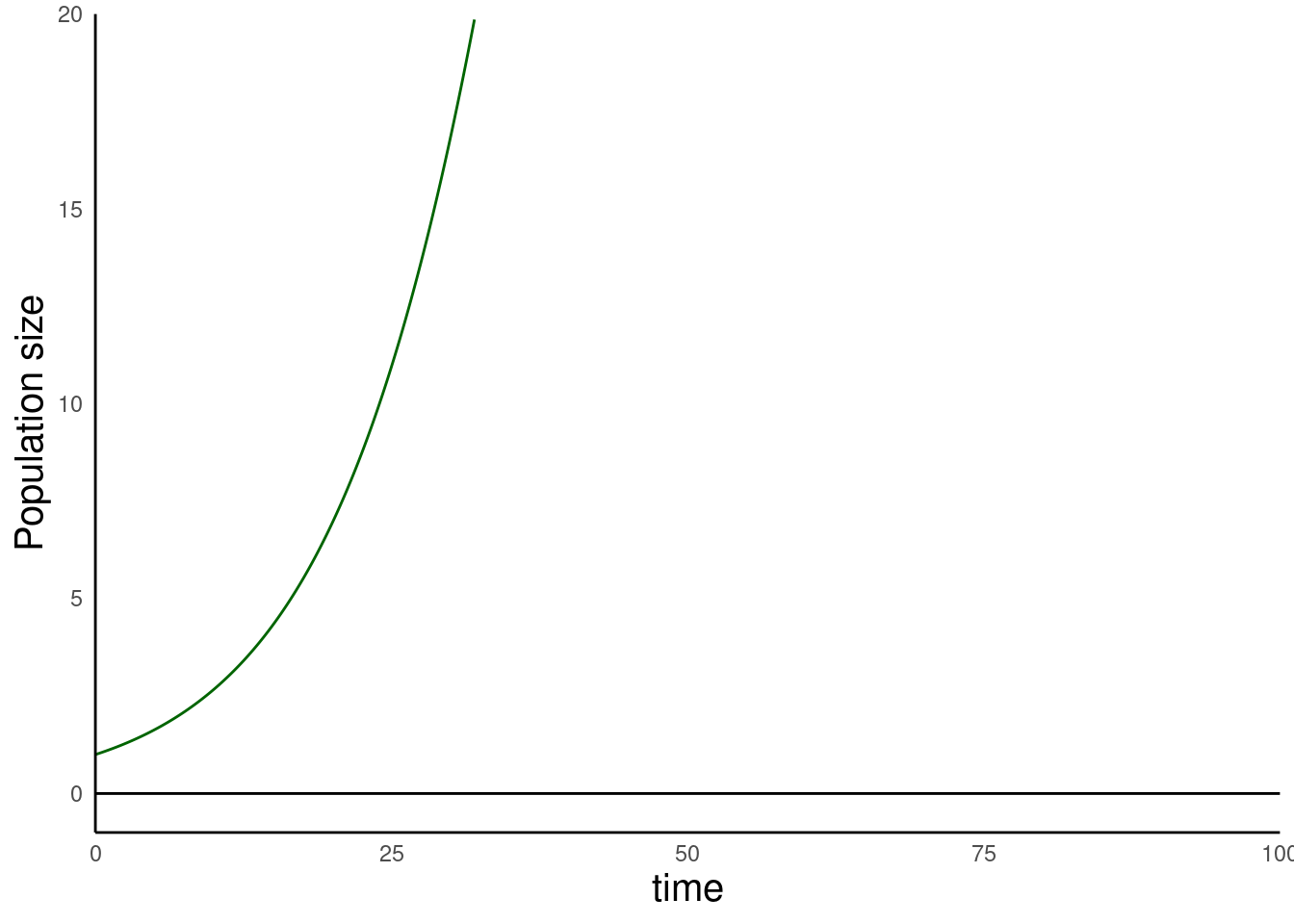
This means the equilibrium \(N = 0\) is an unstable equilibrium

Consider a population that is at equilibrium because \(N = K\)

A small perturbation causes \(N\) to shift slightly lower than \(K\) (e.g. a hurricane that kills a fraction of the individuals)

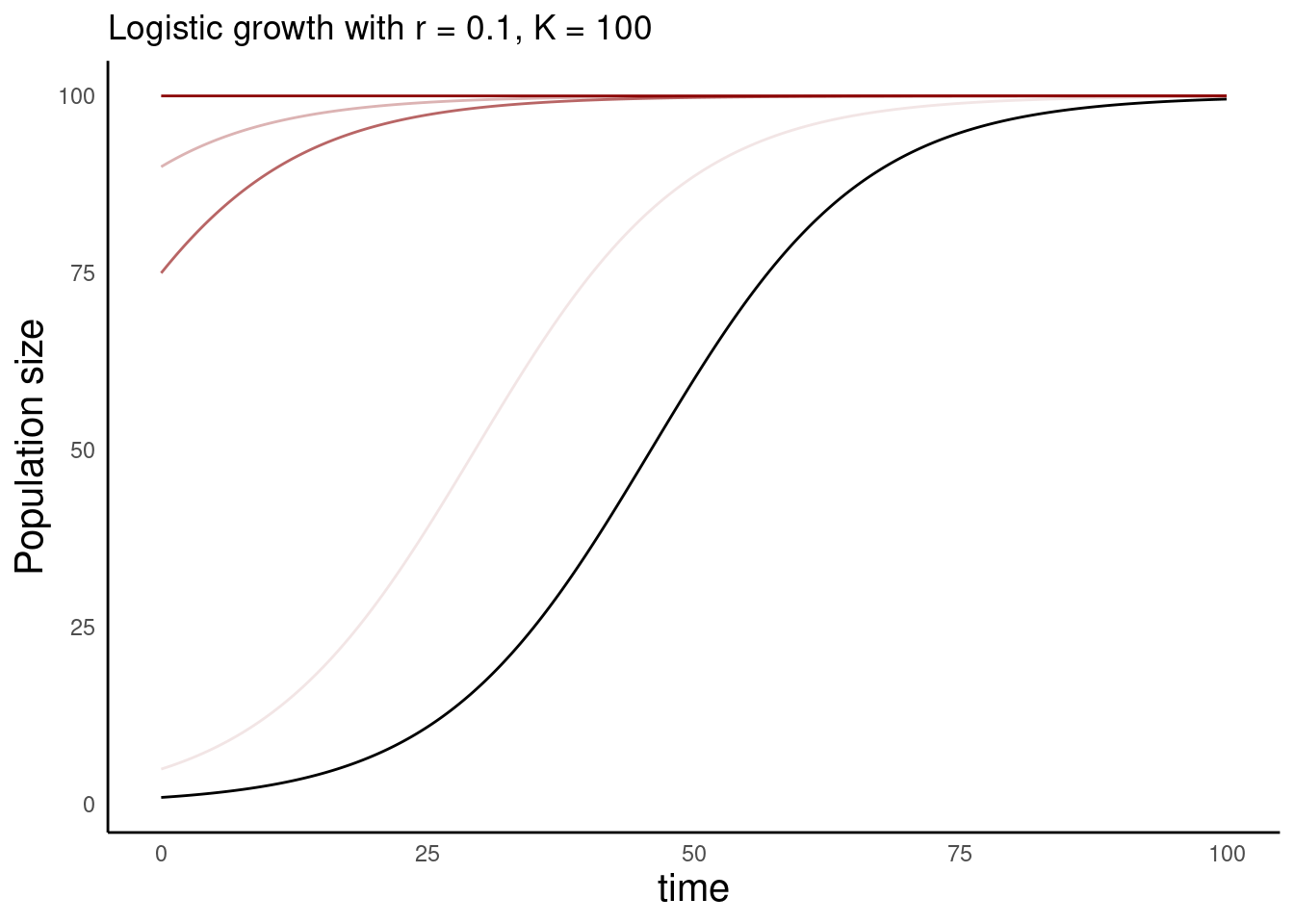
Alternatively, a small perturbation causes \(N\) to shift slightly higher than \(K\) (e.g. humans release additional individuals into the system)

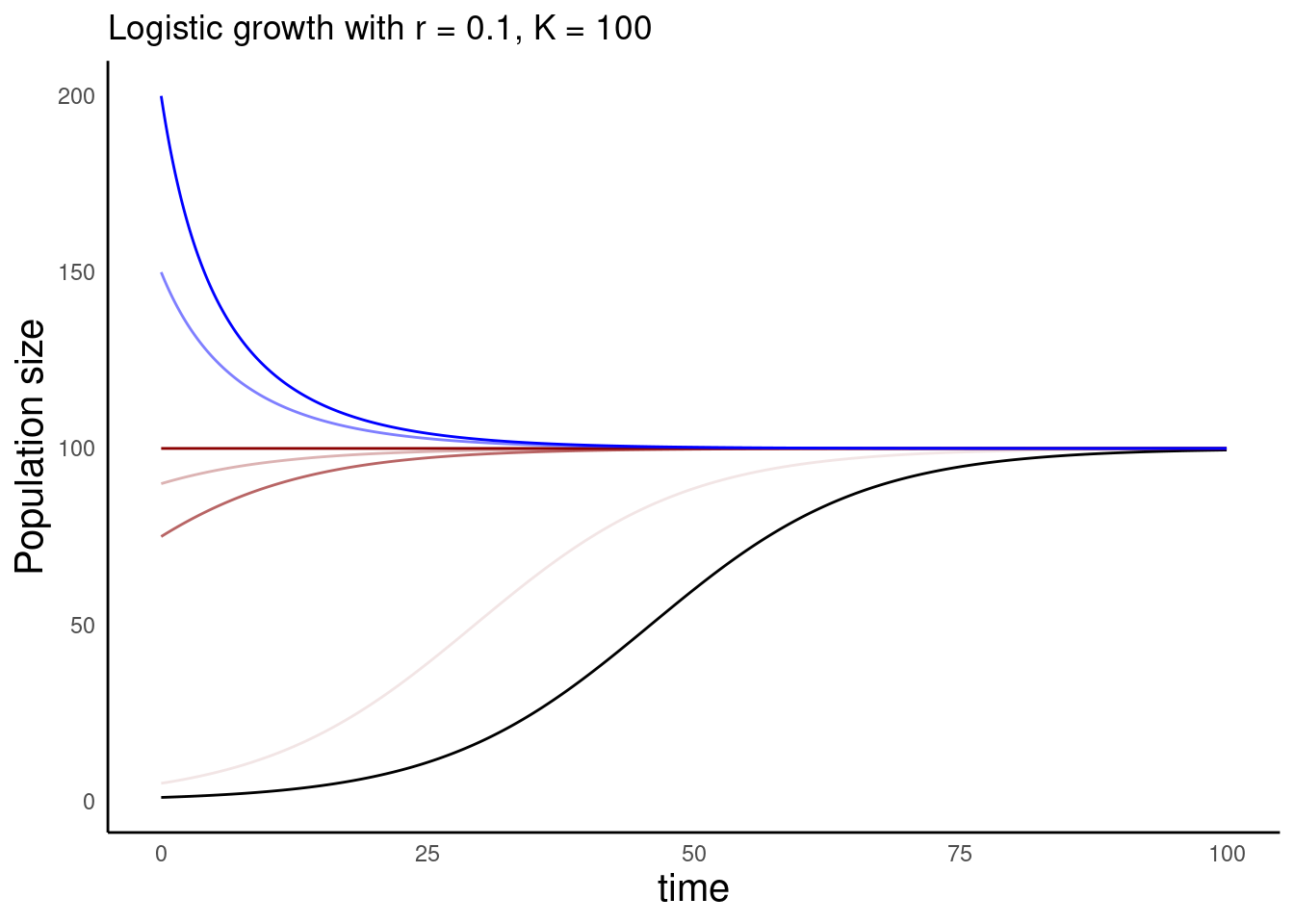
Stability of the logistic equlibrium

• The past few slides show that the initial conditions (\(N\) at \(t=0\)) doesn’t change the equilibrium condition of the system
• This makes it a Stable equilibrium
  • The system is robust to small perturbations

Evaluating assumptions Logistic Growth

One of the implicit assumptions in the logistic growth model is that higher population density always results in reduced per-capita performance

We have discussed many reasons why this may not be true

Incorporate facilitation into logistic growth

• Per-capita growth rate can increase with population size
• Until some threshold, after which it declines again

Density-dependence with Allee effect

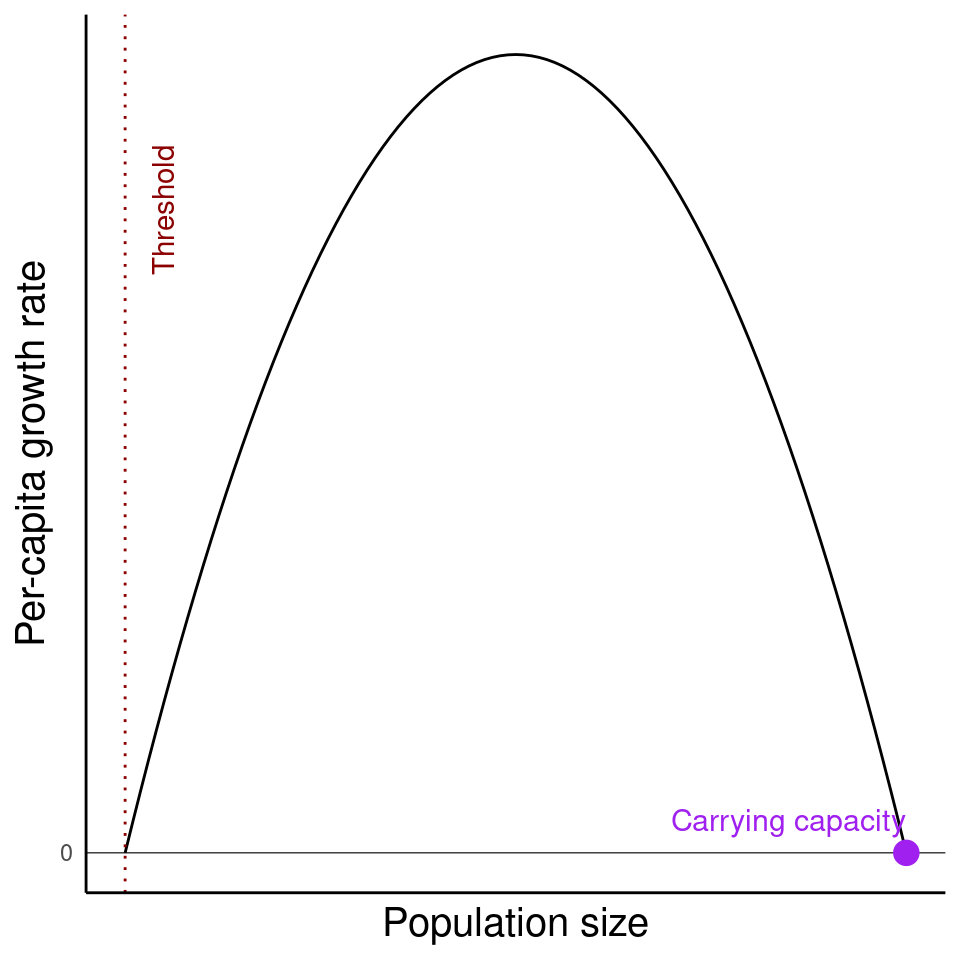
Incorporate facilitation into logistic growth

\[\frac{dN}{dt} = - rN \bigg( 1-\frac{N}{T} \bigg) \bigg( 1-\frac{N}{K} \bigg)\]

\(T\) is a threshold value – when populations are below this, fitness increases with population size

• e.g. There might be a “Threshold” size of a wolf pack
• below this threshold, it is hard to hunt, such that the population crashes to extinction
• above this threshold, the population grows to carrying capacity

Lessons from a model with facilitation

Lessons from a model with facilitation

Lessons from a model with facilitation

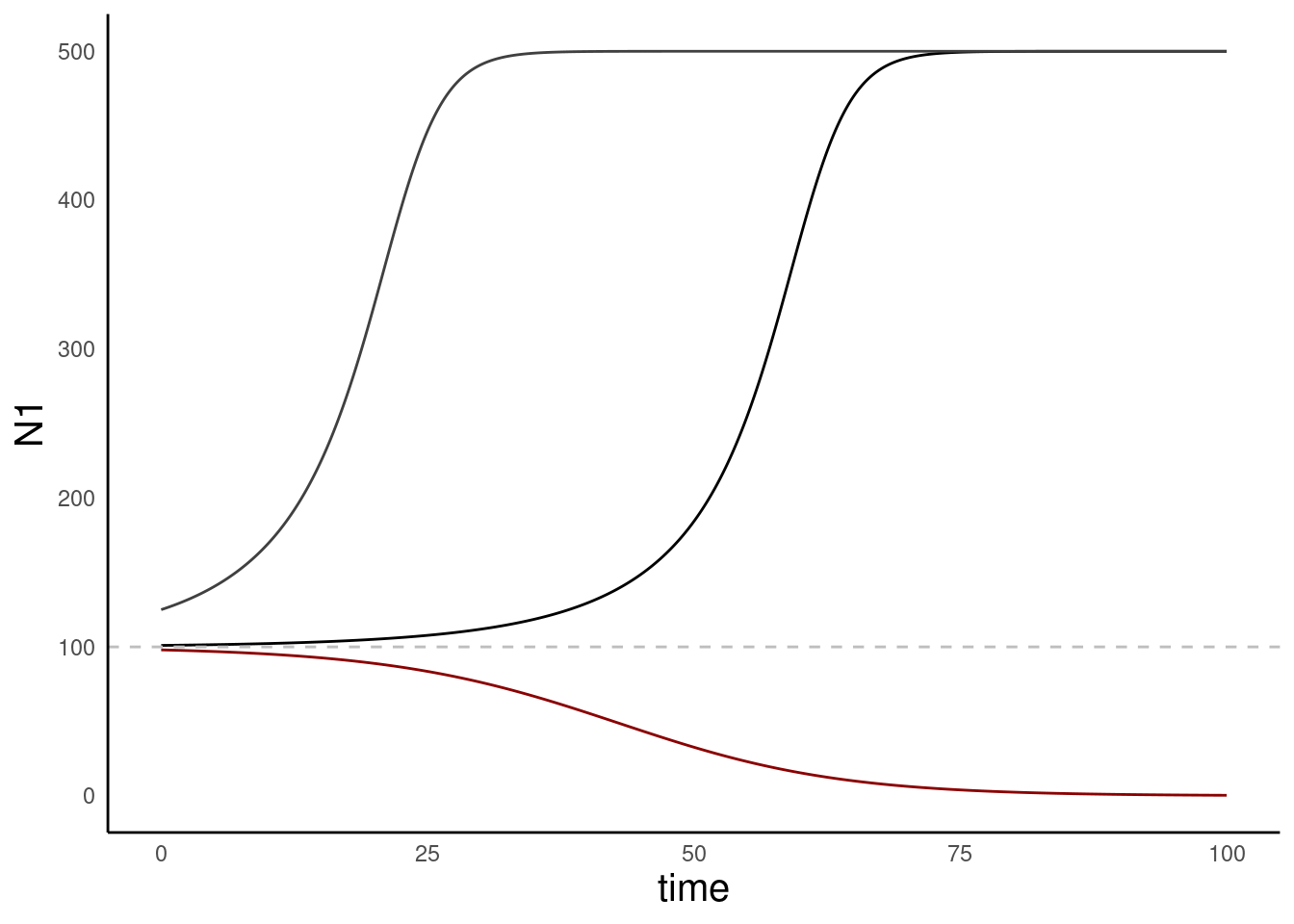
Equilibria and stability

\[\frac{dN}{dt} = - rN \bigg( 1-\frac{N}{T} \bigg) \bigg( 1-\frac{N}{K} \bigg)\]

This model has three equilibrium points:

\(N = 0\), \(N = T\), and \(N = K\)

What do we expect in terms of the stability for each of these equilibrium points?

\(N = 0 \to \text{stable equilibrium}\), \(N = T \to \text{unstable equilibrium}\), \(N = K \to \text{stable equilibrium}\)

Equilibria and stability

\[\frac{dN}{dt} = - rN \bigg( 1-\frac{N}{T} \bigg) \bigg( 1-\frac{N}{K} \bigg)\]

This model has three equilibrium points:

\(N = 0\), \(N = T\), and \(N = K\)

What do we expect in terms of the stability for each of these equilibrium points?

\(\boxed{N = 0 \to \text{stable equilibrium}}\), \(N = T \to \text{unstable equilibrium}\), \(N = K \to \text{stable equilibrium}\)

Density-dependence summary

• Birth and death rates can depend on the size of the population
• When this happens, the population growth rate will also change with population size
• Population growth rate declines linearly with \(N\) in the logistic model
  • This gives rise to a very stable equilibrium…
  • … but it isn’t realistic in all cases
• When we account for Allee effects (birth rates grow or death rates decline with bigger populations, i.e. positive density-dependence), we encounter unstable equilibria
  • Populations falling below the “threshold” crash to extinction