Coexistence in competitive communities
Interspecific competition
Lotka-Volterra competition equations:
\[\frac{dN_1}{dT} = r_1N_1(1-\alpha_{11}N_1 - \alpha_{12}N_2)\]
\[\frac{dN_2}{dT} = r_2N_2(1-\alpha_{21}N_1 - \alpha_{22}N_2)\]
Possible outcomes of two species competing:
- Both species can have stable coexistence
- Species 1 can win, and exclude Species 2
- Species 2 can win, and exclude Species 1
- “It depends” – whichever species comes first, wins in competition.
How to distinguish between the possible options?
Zero net-growth isocline (ZNGI) analysis
Key question: Under what conditions does each species reach equilibrium?
\(\frac{dN_1}{dt} = 0\) and \(\frac{dN_2}{dt} = 0\)
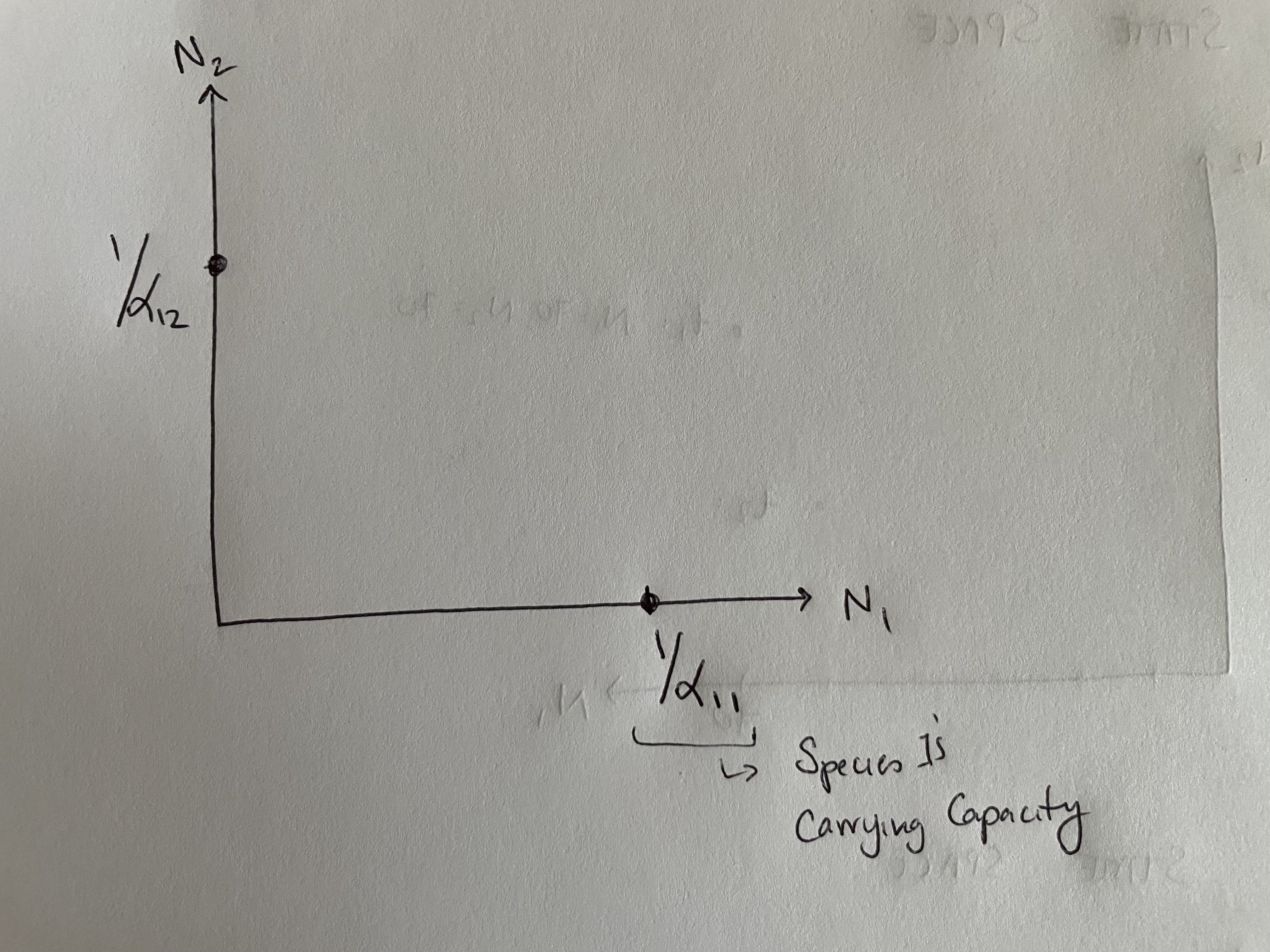
Species 1’s equilibrium analysis:
- \(\frac{dN_1}{dt} = 0\) at two extreme conditions:
- Species 1 is at its carrying capacity, and Species 2 is absent (\(N_1 = 1/\alpha_{11},~ N_2 = 0\))
- Species 2 is very abundant, and Species 1 is nearly absent (\(N_1 = 0,~ N_2 = 1/\alpha_{12}\))
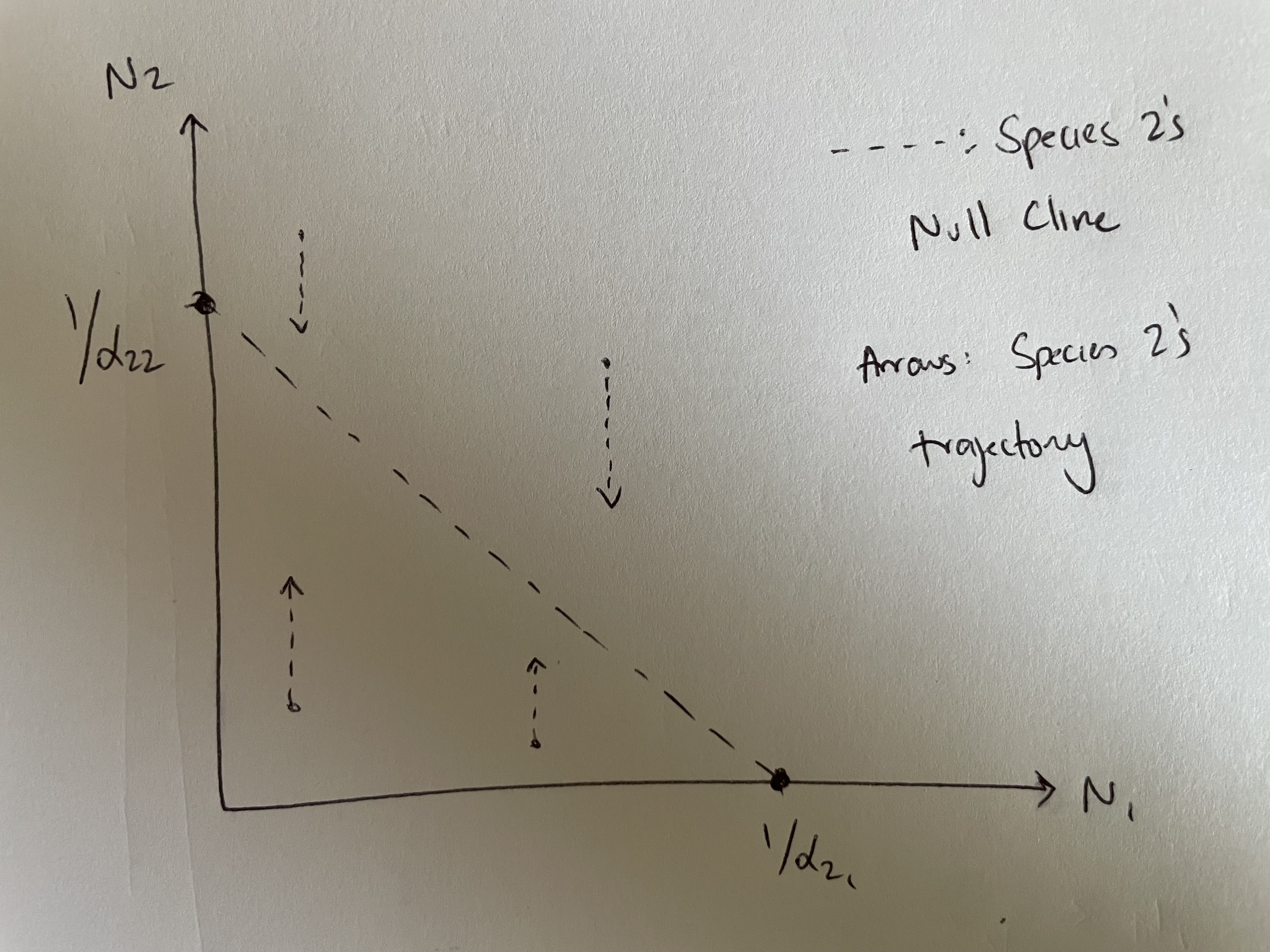
- \(\frac{dN_2}{dt} = 0\) at two extreme conditions:
- Species 2 is at its carrying capacity, and Species 1 is absent (\(N_1 = 0,~ N_2 = 1/\alpha_{22}\))
- Species 1 is very abundant, and Species 2 is nearly absent (\(N_1 = 1/\alpha_{21}, ~ N_2 = 0\))
Visualizing the equilibrium points
Species 1’s equilibrium analysis:
- Species 1 is at its carrying capacity, and Species 2 is absent (\(N_1 = 1/\alpha_{11},~ N_2 = 0\))
- Species 2 is very abundant, and Species 1 is nearly absent (\(N_1 = 0,~ N_2 = 1/\alpha_{12}\))
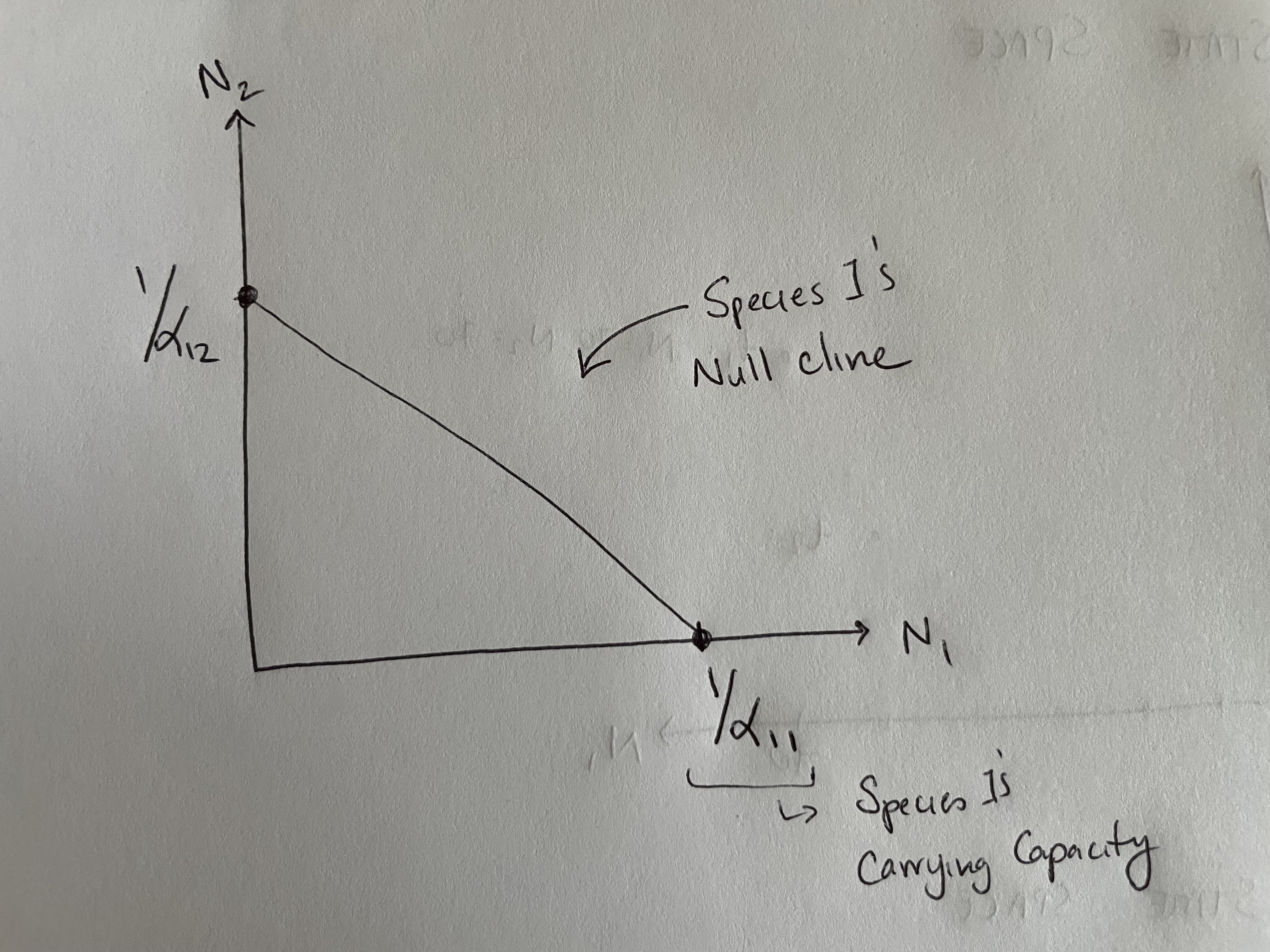

Visualizing the equilibrium points
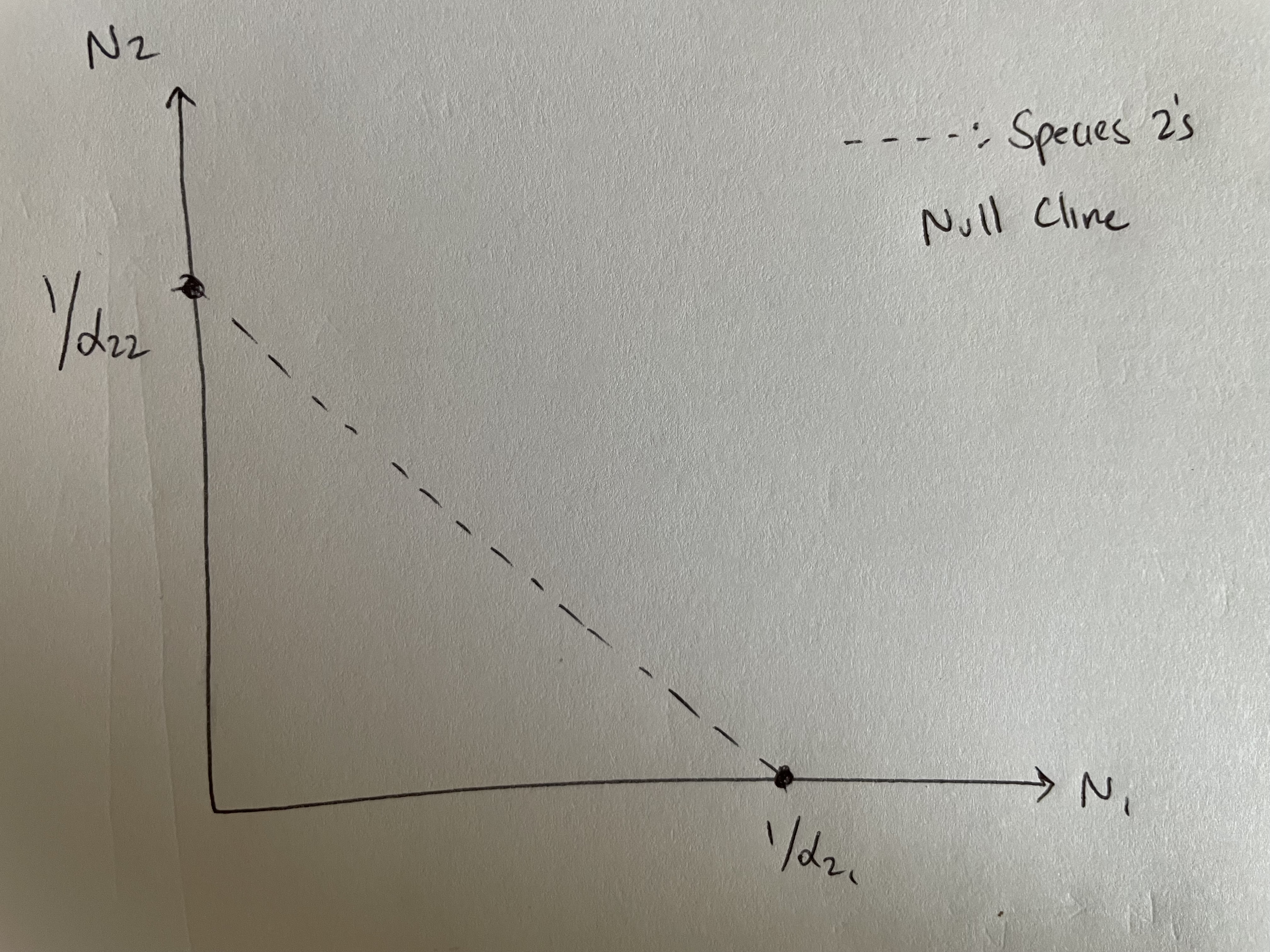
Species 2’s equilibrium analysis:
Species 2 is at its carrying capacity, and Species 1 is absent (\(N_1 = 0,~ N_2 = 1/\alpha_{22}\))
Species 1 is very abundant, and Species 2 is nearly absent (\(N_1 = 1/\alpha_{21}, ~ N_2 = 0\))
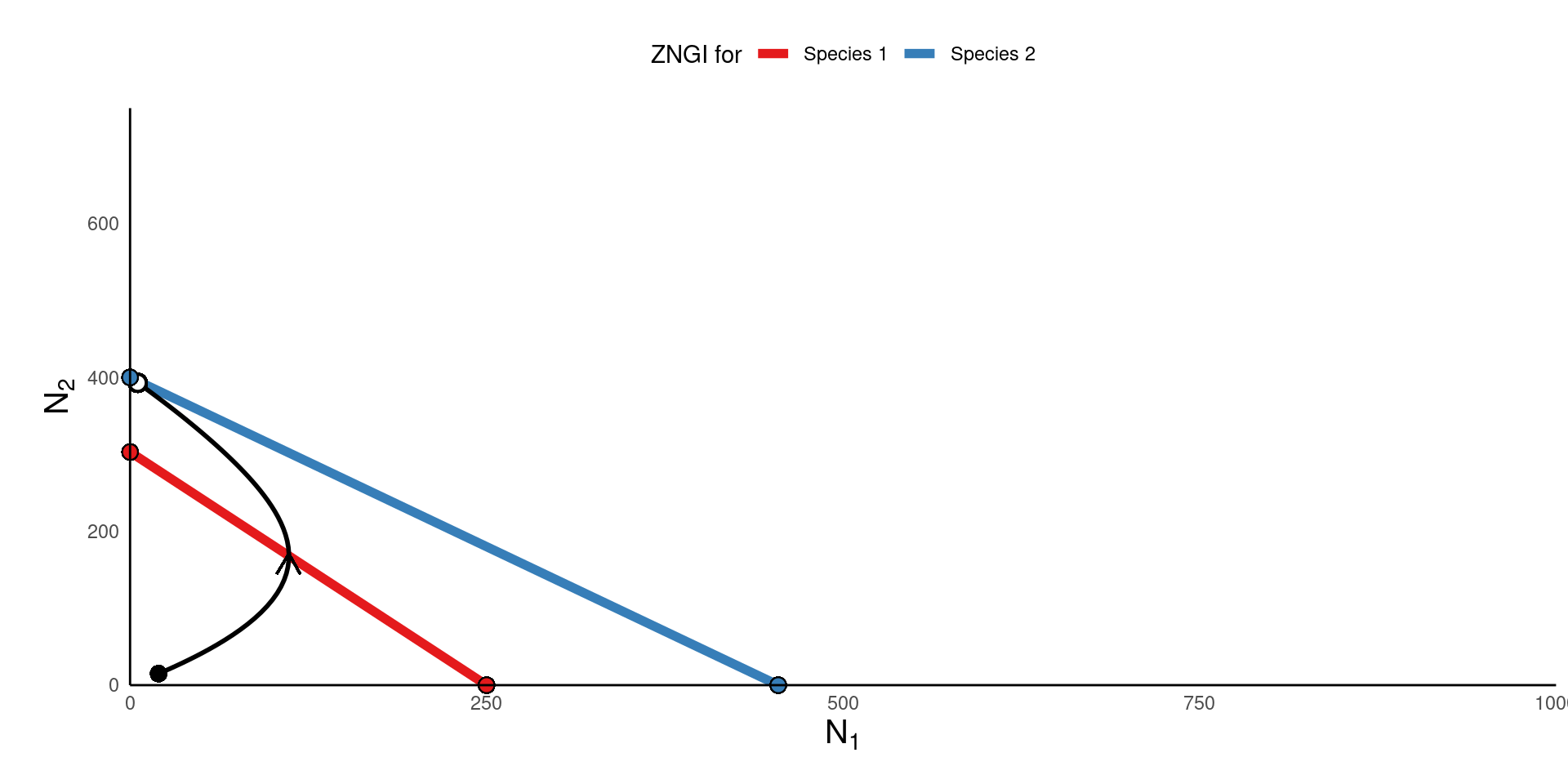
Jointly visualizing both species’ isoclines
Putting numbers to the variables
Consider the following interaction coefficients:
\[\alpha_{11} = 0.005;~ \alpha_{12} = 0.002;~ \alpha_{22} = 0.007;~ \alpha_{21} = 0.002\]
\[1/\alpha_{11} = 200;~ 1/\alpha_{12} = 500;~ 1/\alpha_{22} = 142;~ 1/\alpha_{21} = 500\]
Putting numbers to the variables
Consider the following interaction coefficients:
\[\alpha_{11} = 0.005;~ \alpha_{12} = 0.002;~ \alpha_{22} = 0.01;~ \alpha_{21} = 0.007\]
\[1/.005 = 200;~ 1/.002 = 500;~ 1/.01 = 100;~ 1/.007 = 142\]
Recall that the equilibrium points for the two species are:
- Species 1: (\(N_1 = 1/\alpha_{11},~ N_2 = 0\)) and (\(N_1 = 0,~ N_2 = 1/\alpha_{12}\))
- Species 2: (\(N_1 = 0,~ N_2 = 1/\alpha_{22}\)) and (\(N_1 = 1/\alpha_{21},~ N_2 = 0\))
Your turn
- Draw the isoclines for a pair of species whose interaction coefficients are as follows:
\[\alpha_{11} = 0.008;~ \alpha_{12} = 0.008;~ \alpha_{22} = 0.006;~ \alpha_{21} = 0.005\]
\[1/0.008 = 125;~ 1/0.008 = 125;~ 1/.006 = 166;~ 1/.005 = 200\]
Your turn
- Draw the isoclines for a pair of species whose interaction coefficients are as follows:
\[\alpha_{11} = 0.002;~ \alpha_{12} = 0.005;~ \alpha_{22} = 0.002;~ \alpha_{21} = 0.007\]
\[1/.002 = 500;~ 1/.005 = 200;~ 1/.002 = 500;~ 1/007 = 142\]
Recall that the equilibrium points for the two species are:
- Species 1: (\(N_1 = 1/\alpha_{11},~ N_2 = 0\)) and (\(N_1 = 0,~ N_2 = 1/\alpha_{12}\))
- Species 2: (\(N_1 = 0,~ N_2 = 1/\alpha_{22}\)) and (\(N_1 = 1/\alpha_{21},~ N_2 = 0\))
Coexistence under competition
Possible outcomes in Lotka-Volterra competition
- Both species can coexist
- If each species limits itself more than it limits the other
- More “intra-specific competition” than “inter-specific competition”
- Species 1 wins, while Species 2 is excluded
- Species 2 wins, while Species 1 is excluded
- “It depends”
We are often interested in understanding how it is that species can coexist
- Organisms need basically the same set of resources, yet in many systems we see lots of diversity
- Alternatively, this diversity is challenged in some systems, e.g. due to species invasions.
- So, how can competition promote coexistence?
Possible outcomes under competition:
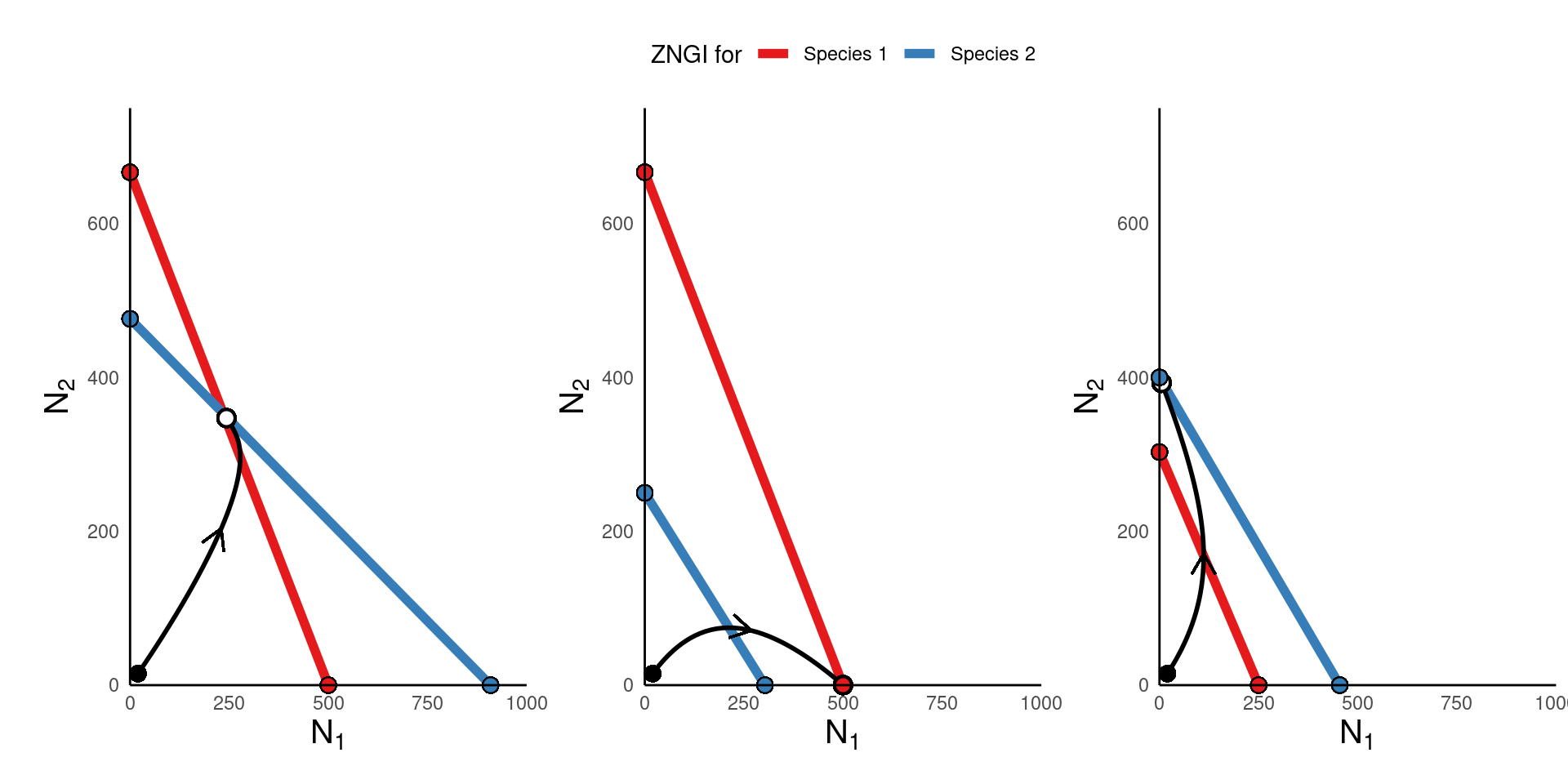
- We also saw “it depends” as an outcome – let’s hold off on that one for now.
- What gives rise to scenario 1 (coexistence) vs. scenarios 2 or 3 (competitive dominance)?
Making sense of competitive dominance
- Let’s start with competitive dominance, as it is conceptually more straightforward
- Dominance will happen whenever one isocline is “outside” the other, i.e. no intersection
- There can be no condition under which \(\frac{dN_1}{dt} = 0\) AND \(\frac{dN_2}{dt} = 0\), which means no equilibrium possible with both species
- So, the only equilibrium points are when one species is absent.
Why would one isocline be “outside” another?
Why would one isocline be “outside” another?
- Consider a case where species 2 “wins”:
Why would one isocline be “outside” another?
- Consider a case where species 2 “wins”:
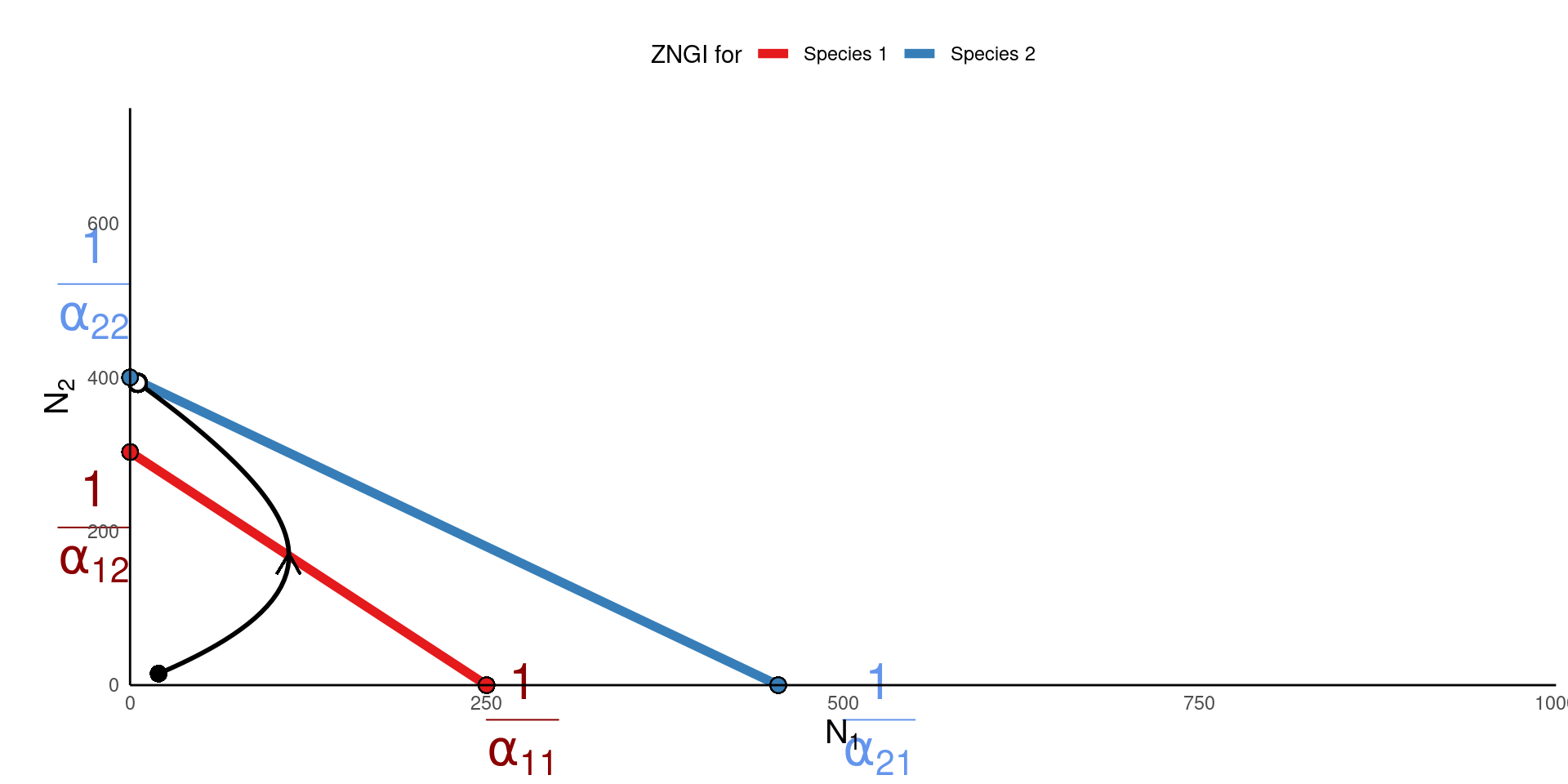
Why would one isocline be “outside” another?
- Consider a case where species 2 “wins”:
Why would one isocline be “outside” another?
- Consider a case where species 2 “wins”:
Species 1 is strongly limited by Species 1, AND
it is strongly limited by Species 2
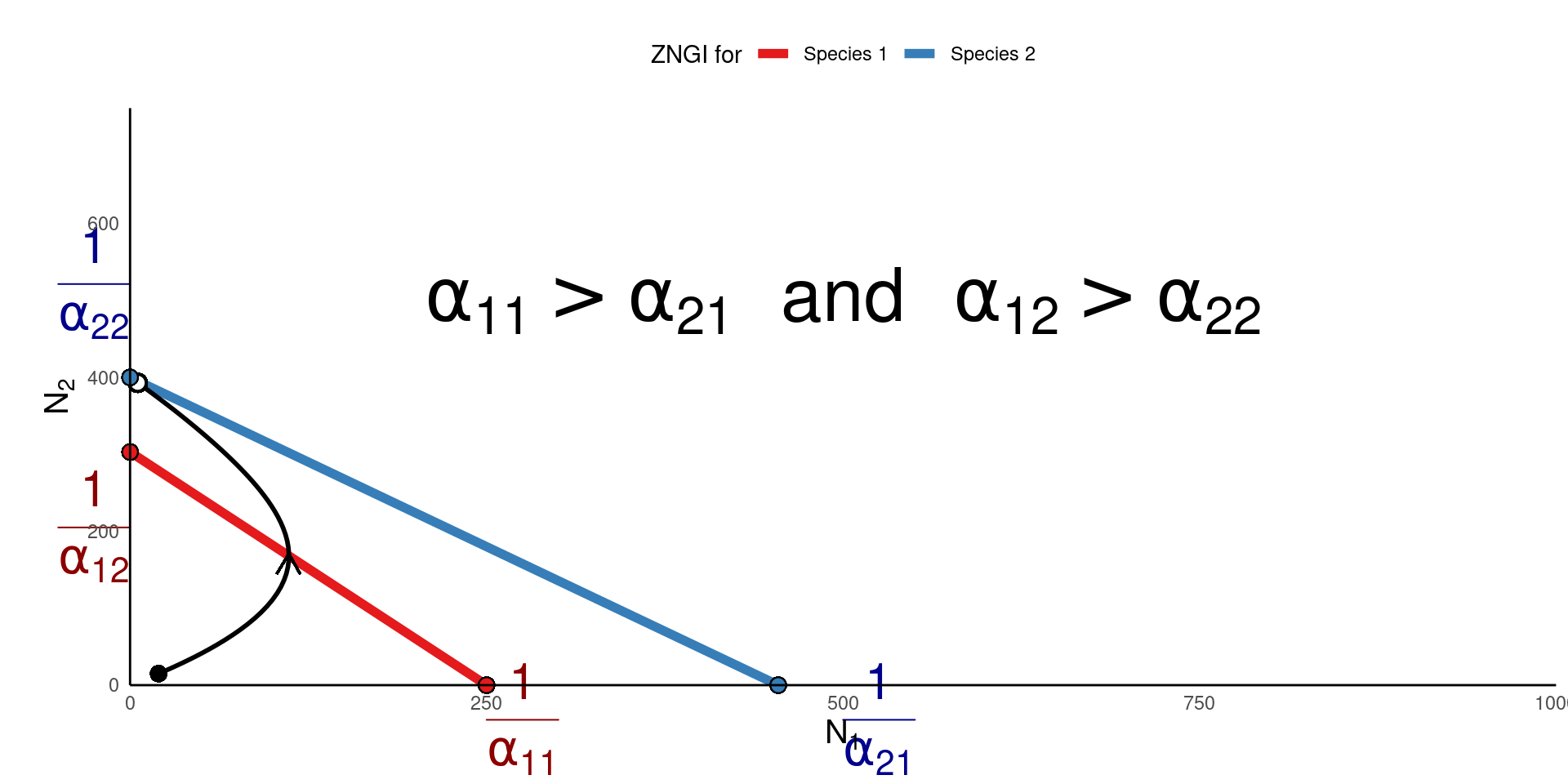
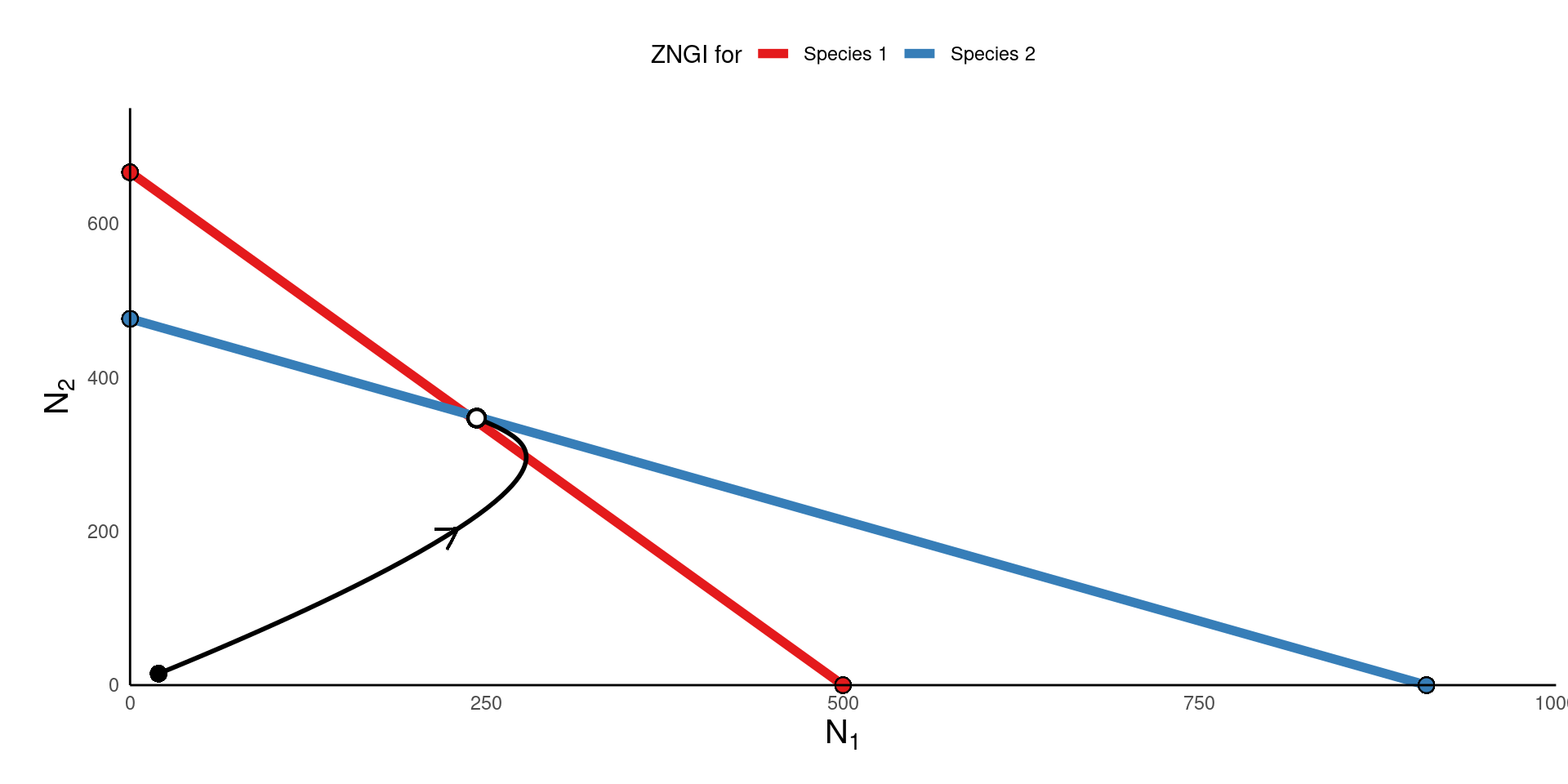
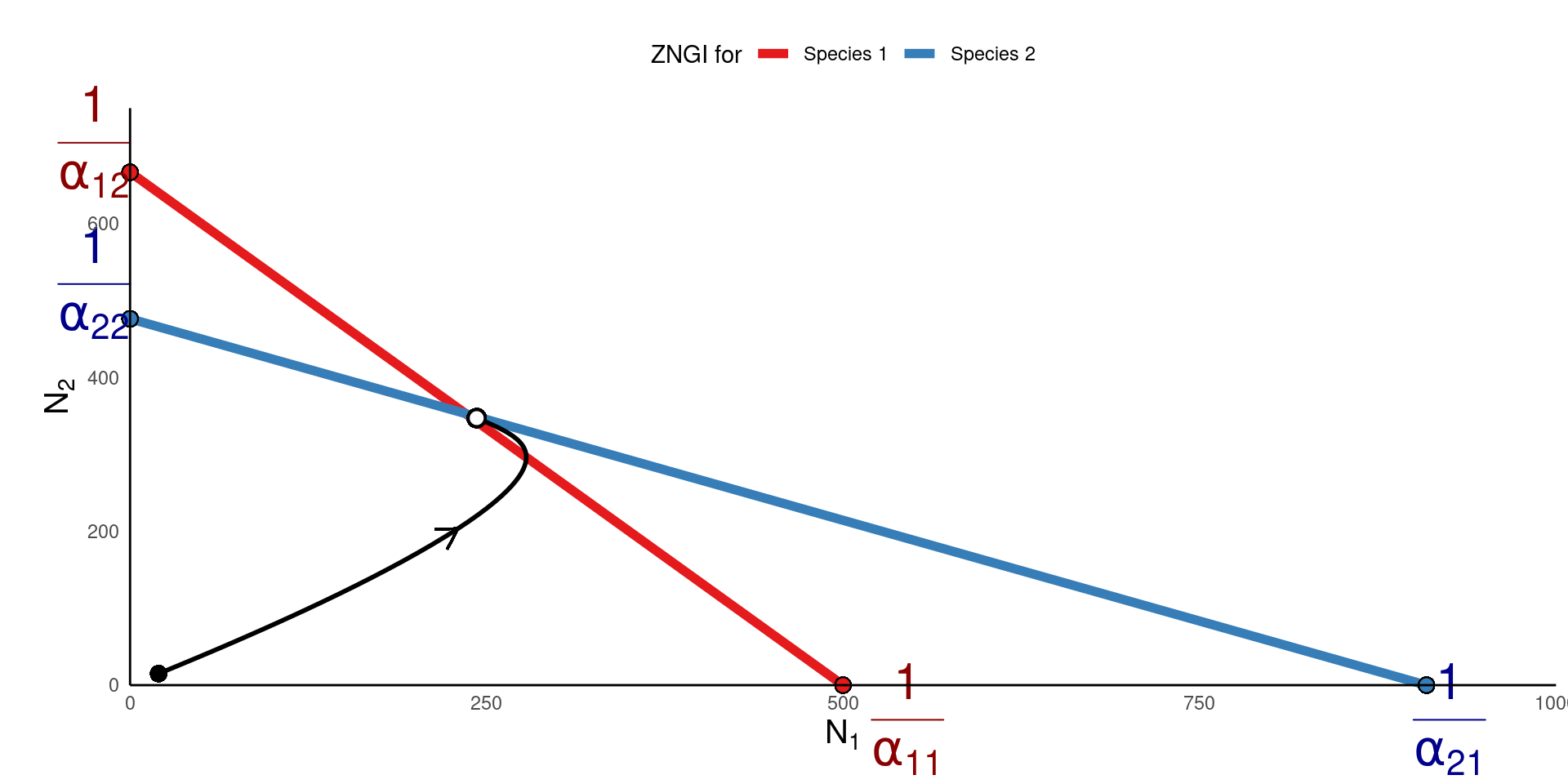
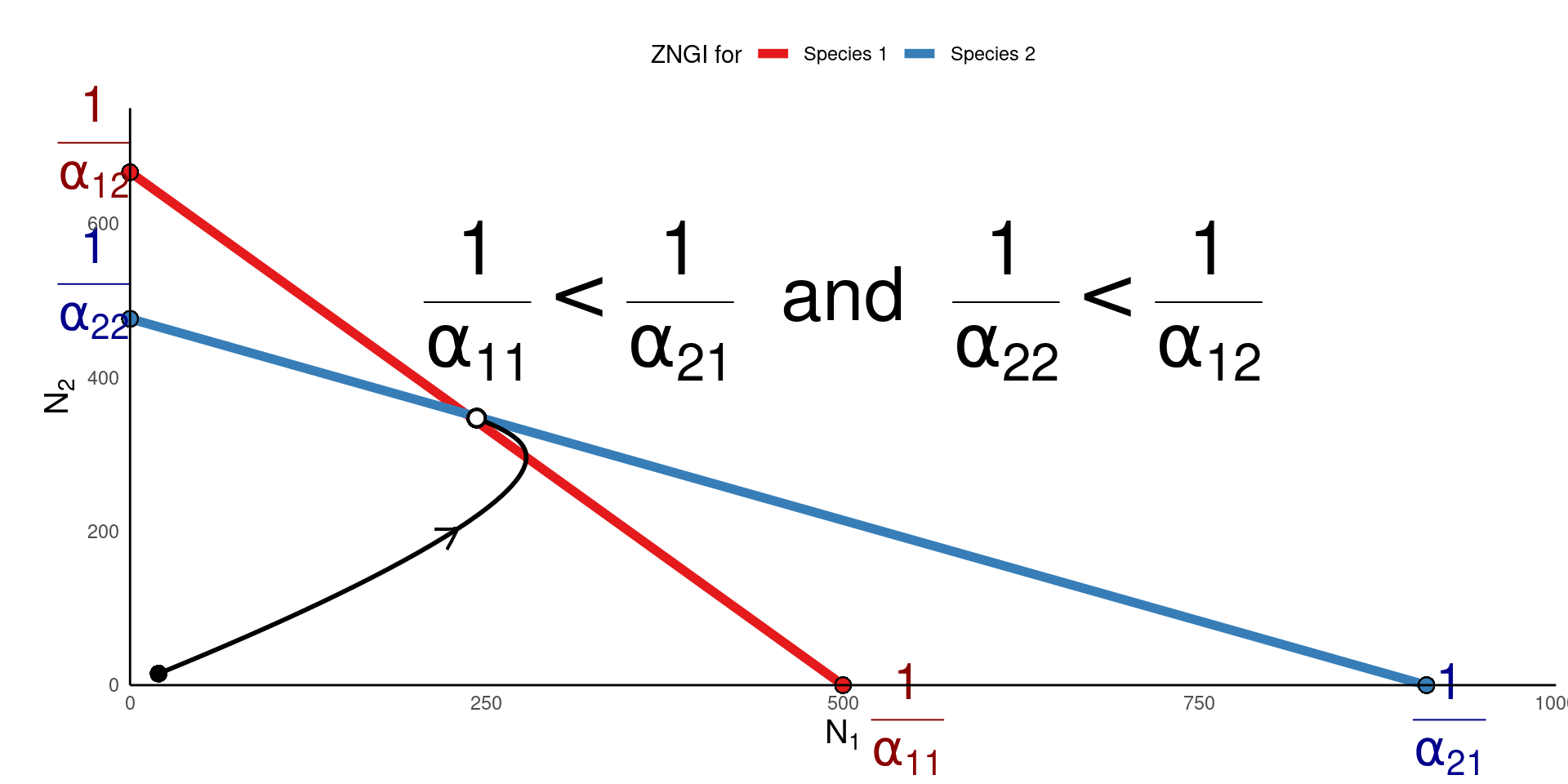
What supports species coexistence?
Let’s follow a similar logic for understanding why competition could support coexistence
What supports species coexistence?
What supports species coexistence?
What supports species coexistence?
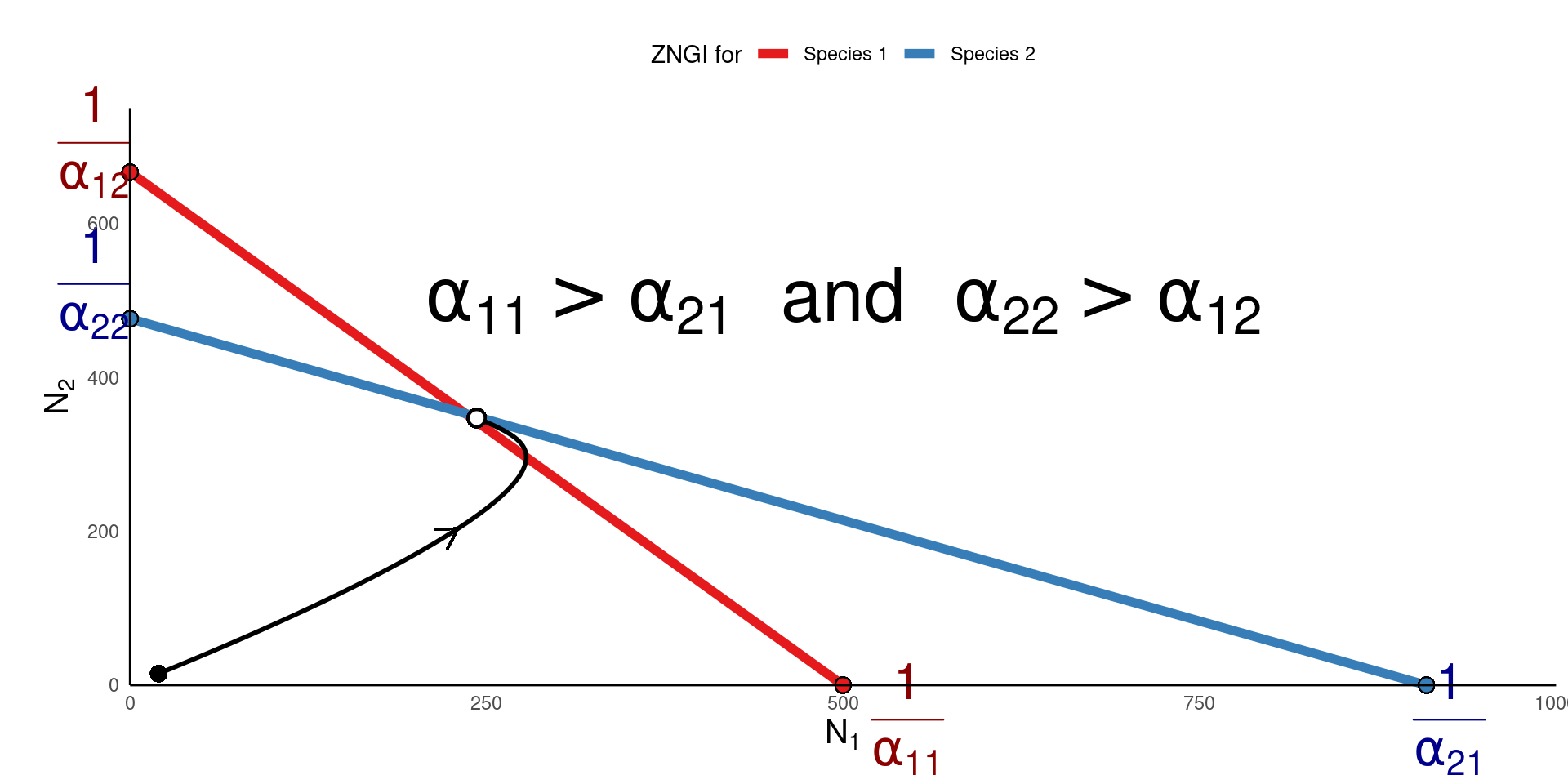
Biologically, this means that for coexistence to occur, each species should limit itself more than it limits the other
- When would this happen?
- If species have distinct niches, competition might be stronger within a niche than between niches.
Conclusion:
Coexistence in competitive communities
Photo by Gaurav, of Tejon Ranch in southern California
Why study species coexistence?
- Ecological systems are often incredibly diverse
- But sometimes, they are not – as in the case of species invasion rapidly eroding biodiversity
- So, the question arises: Why can certain species coexist, but others cannot?
Photo by Gaurav, of Tejon Ranch in southern California
How to study coexistence?
- There’s often lots of species coexisting, but we can take a reductionist approach
- Model the dynamics of two species at a time
- Analyze whether the species can coexist at equilibrium
- Graphical analysis using zero-net growth isoclines on Phase Spaces
Photo by Gaurav, of Tejon Ranch in southern California
How to move beyond this reductionist approach
- Extending the competition model to many species within a guild
- Matrix math, but this extension is very much based on the same principles of equilibrium and stability
- How do interactions across different guilds affect coexistence?
- E.g. can predators affect coexistence of two prey species?
- E.g. can fungal mutualists affect the coexistence of tree species? (focus of Gaurav’s PhD research)
- How can we conduct experiments to quantify these effects?
Coexistence under competition
Competitive coexistence
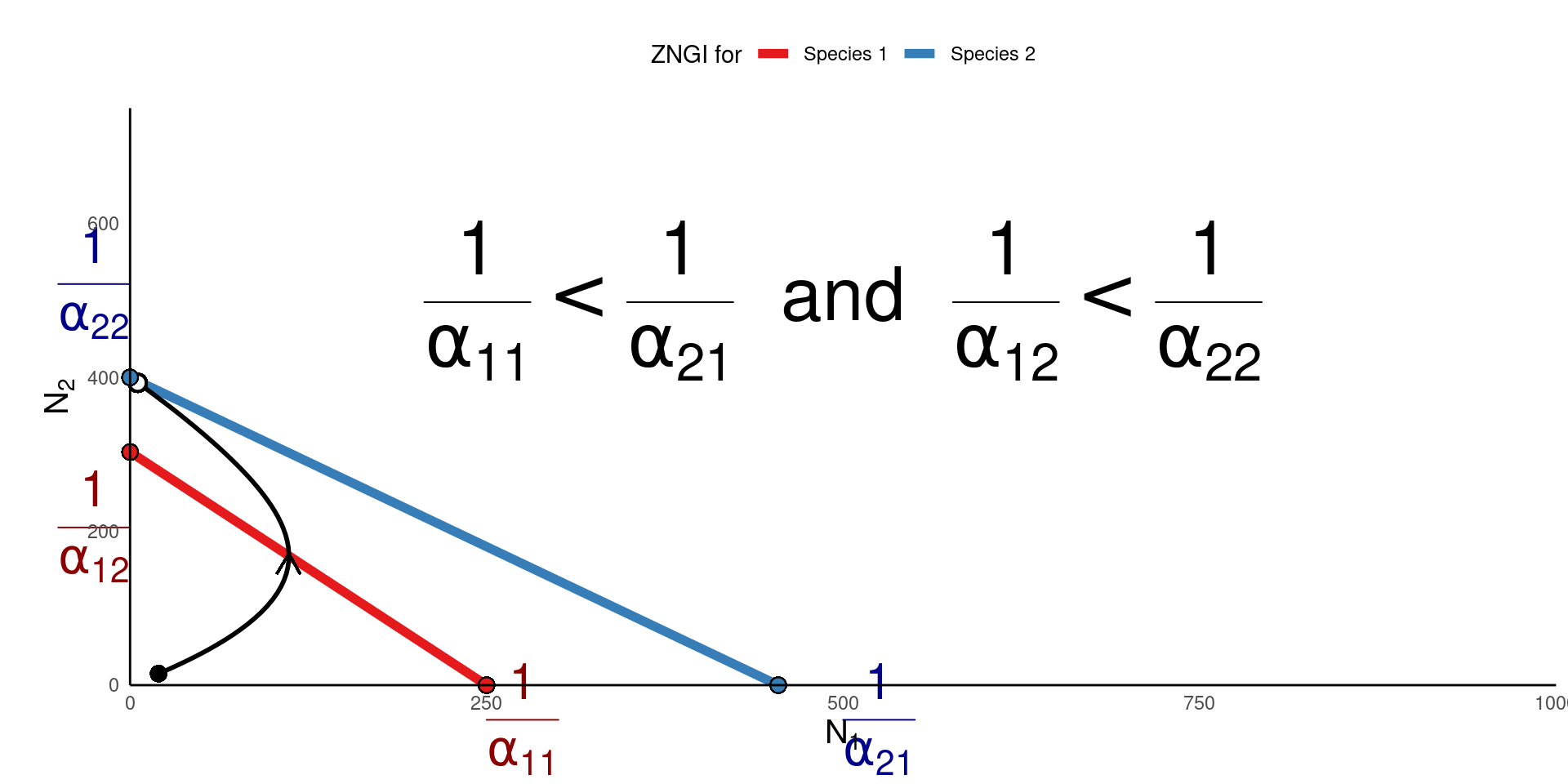
Coexistence can happen when:
- Individuals limit members of their own species more than other species
- \(\alpha_{11} > \alpha_{21}\) and \(\alpha_{22} > \alpha_{12}\)
- This is expected when there is some degree of “niche separation” among species
- Coexistence is limited if one species experiences the brunt of competition and the other doesn’t
- If this is true, then one of the isoclines will be “inside” the other – no coexistence equilibrium exists.
What gives rise to niche separation?
- Classically, resource separation
- E.g. two herbivore species eat grass, but each has its preferred grass
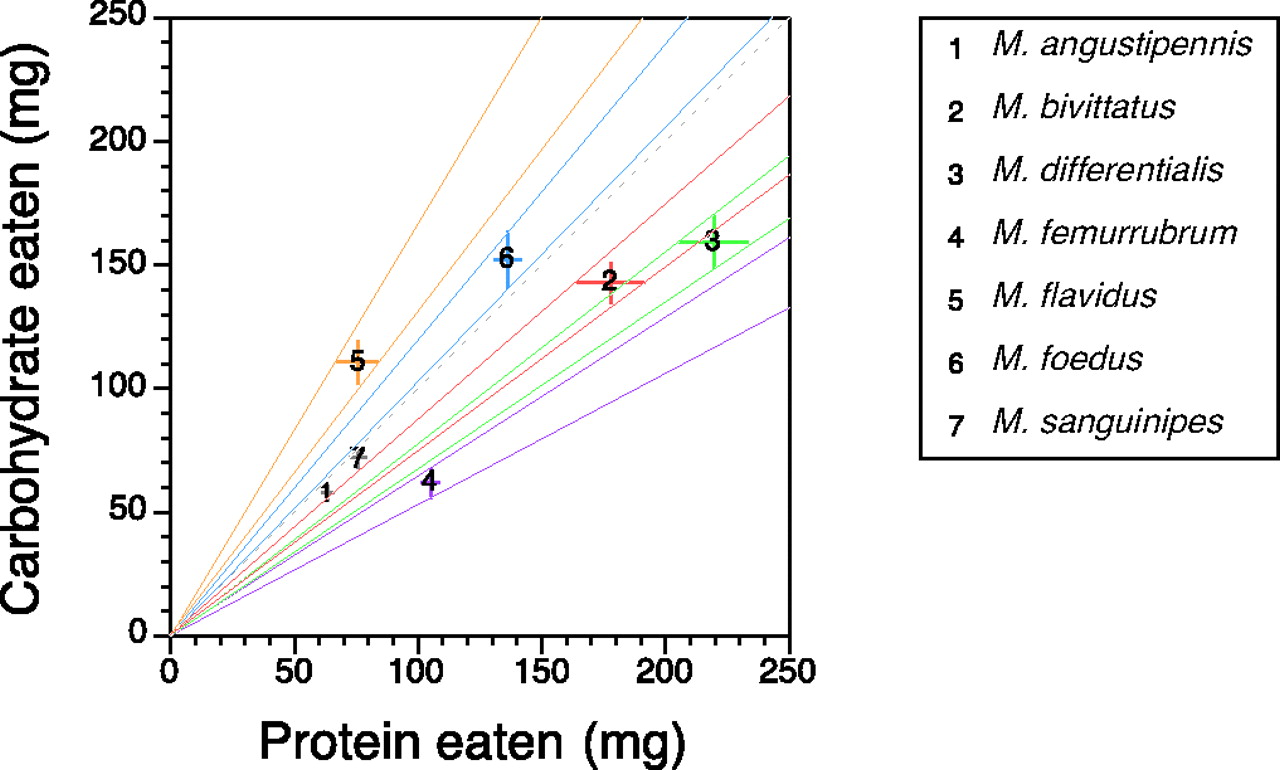
From Behmer and Joern 2008, PNAS
What gives rise to niche separation?
- Time is also a resource
- E.g. two plants need the exact same set of resources, but one active in early-spring and other in late-spring
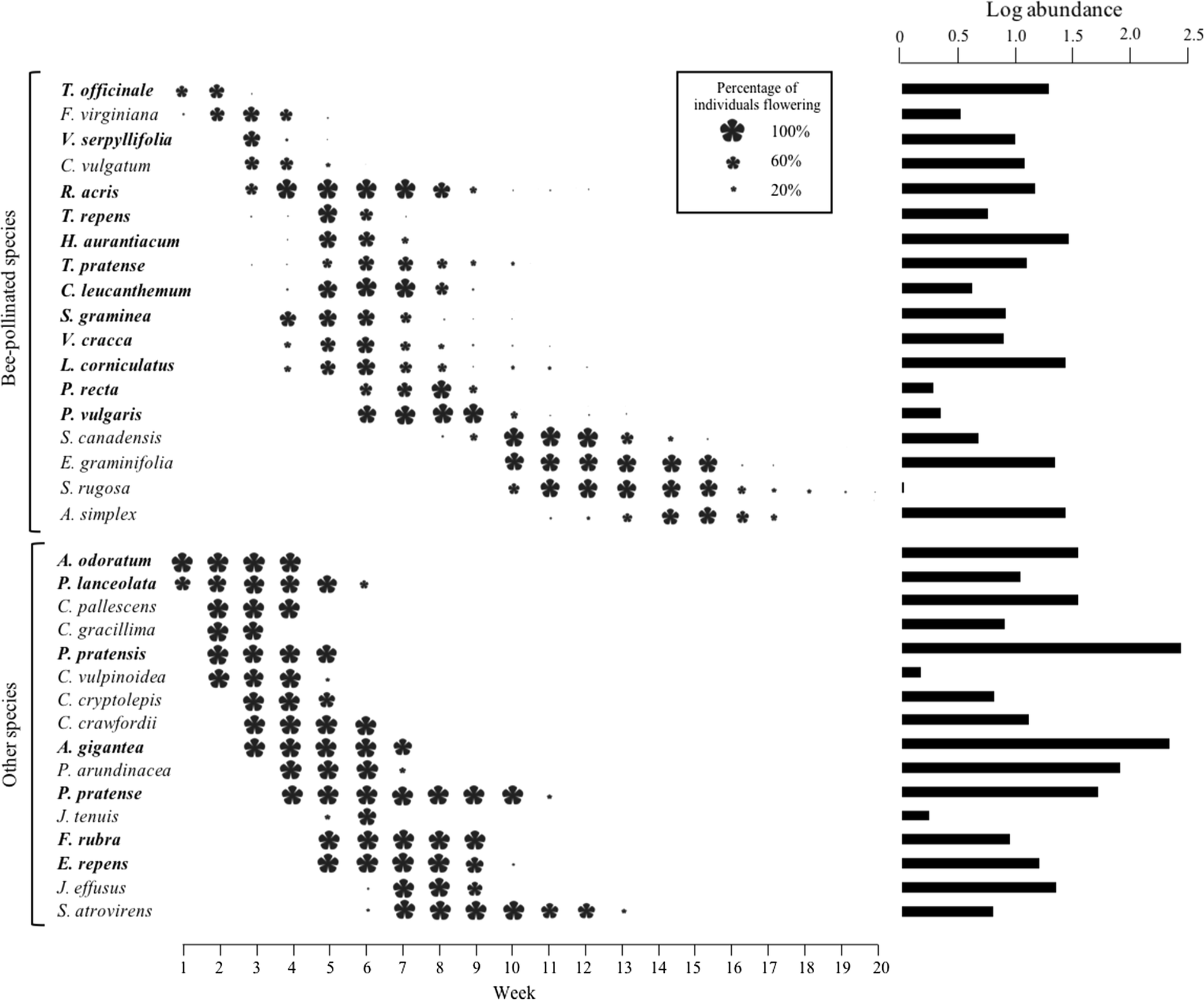
From Jensen et al. 2019, Oecologia
What gives rise to niche separation?
- Space is also a resource
- E.g. two birds eat similar insects, but primarily hunt in distinct microhabitats

from Kent and Sherry 2022 Ecology (based at Tulane Univ.)
Other mechanisms
- Feedbacks between plants and microbes in the soil


Current state
- Soil microbial feedbacks shape plant coexistence in all terrestrial ecosystems
- But in some cases they promote coexistence (\(\alpha_{11} > \alpha_{21}\) and \(\alpha_{22} > \alpha_{12}\)), and in other cases they promote exclusion
- Understanding how this happens, which microbes are driving the effects, and how this is affected by climate warming, drought, fires, nutrient enrichment remains an open question.
Next week
- Moving beyond pairwise competition, to think about other interactions in communities
- Consumer–resource (e.g. predator-prey, herbivore-prey) and disease dynamics