Organisms as resources and consumers
Part 2

Overarching questions in Consumer–resource dynamics

  • What allows persistence of consumers and resources in the long term?
    • Are there conditions in which consumers “over-consume” and engineer their own demise?
    • How does perturbation of the system (e.g. removal of a “top predator”) affect the network as a whole?

Review from Wednesday

  • Simple models as “building blocks” for more complicated systems

Consider a system with two species (\(R_1\) and \(R_2\)) that compete with one another for resources, but that are also predated on by the same predator (\(C\)).

Write a model that captures the interactions in this system.

For competing species \(R_1\) and \(R_2\):

\[\frac{dR_1}{dt} = r_1R_1(1-\alpha_{11}R_1 - \alpha_{12}R_2)\] \[\frac{dR_2}{dt} = r_2R_2(1-\alpha_{22}R_2 - \alpha_{21}R_1)\]

Modify these to account for consumer effects:

\[\frac{dR_1}{dt} = r_1R_1(1-\alpha_{11}R_1 - \alpha_{12}R_2)-a_1R_1C\] \[\frac{dR_2}{dt} = r_2R_2(1-\alpha_{22}R_2 - \alpha_{21}R_1)-a_2R_2C\]

The consumer equation also needs to reflect both sources of food:

\[\frac{dC}{dt} = e_1 a_1 R_1 C + e_2 a_2 R_2 C - mC\]

  • In the reductionist tradition, we can use these building blocks to logically think through the types of communities that might exist in nature

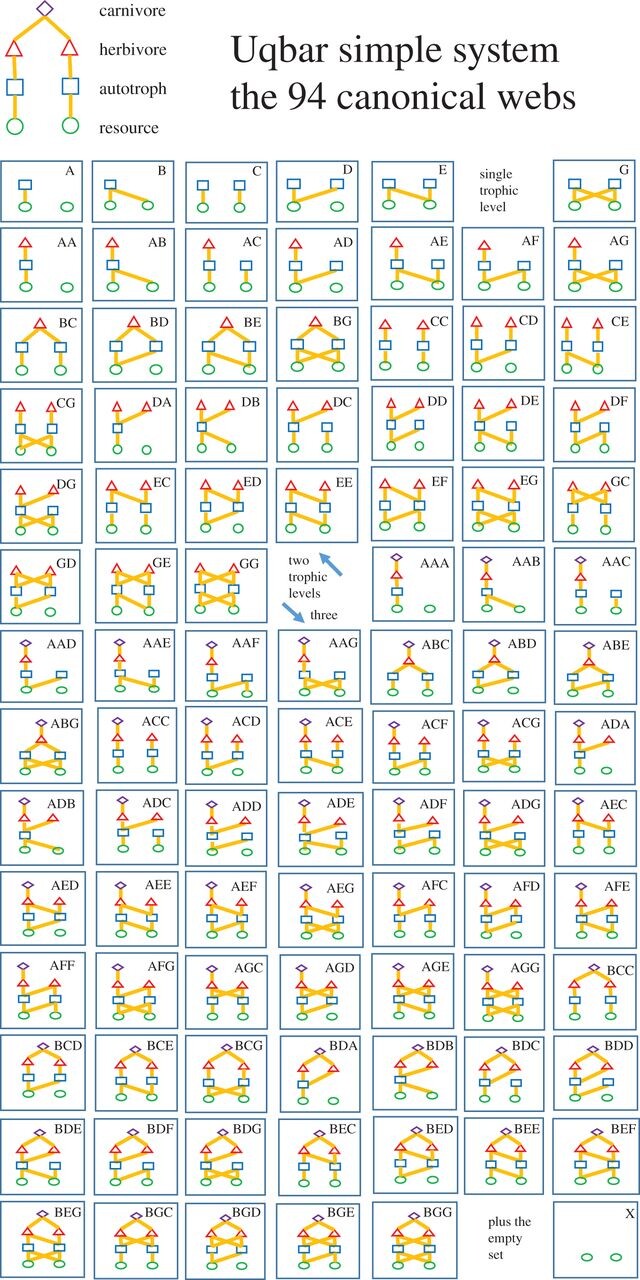
Figure from Bell and Fortier-Dubois 2017, Proc B

Such simplification enables predictions, e.g. what should we expect to happen if one of the herbivores is eliminated?

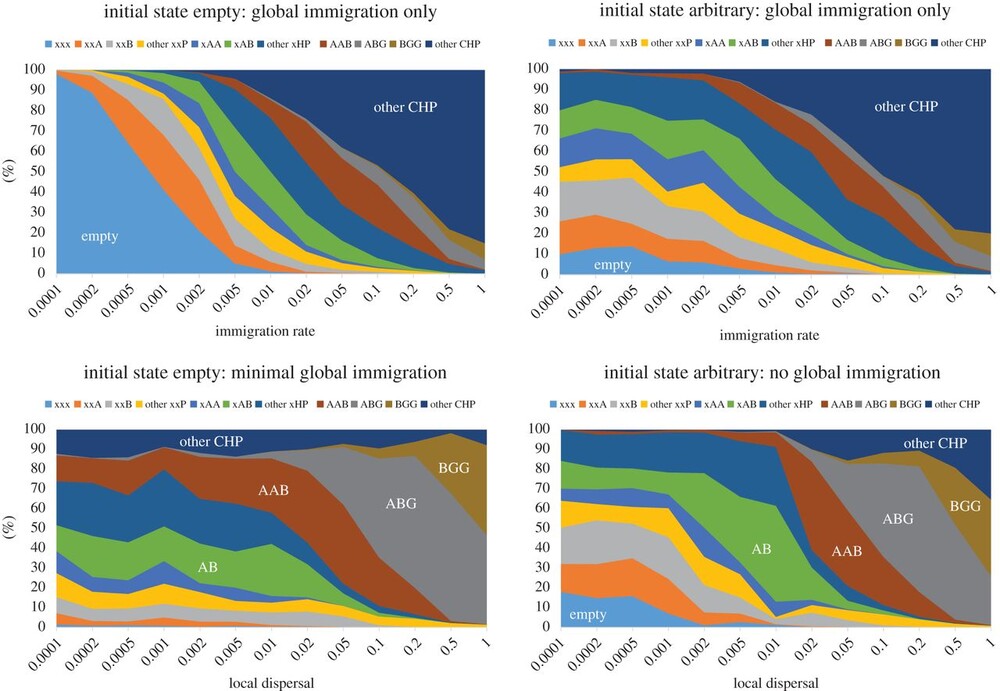
Figure from Bell and Fortier-Dubois 2017, Proc B

Of course, there’s some limit to how complicated a system we can reasonably model

  • We will begin discussing less reductionist approaches next week.

Three-trophic system

  • One producer, an herbivore, and a carnivore

  • e.g. Kelp, sea urchins, and otters

  • Watch the following two videos if you missed Wednesday

How would we model this?

  • Write a simple model of the kelp–urchin–otter system

Assumptions:

  • Kelp experiences exponential growth but gets consumed by urchins
  • Urchins specialize on kelp as their food source, and are consumer by otters
  • Otters primarily eat otters, but they also consume other prey species (e.g. various fish species)

General approach

  • Identify the state variables (in our case, \(K\)elp, \(U\)rchin, \(O\)tter)
  • Determine what assumptions you are willing to make about the system
  • Use our building blocks to start putting together a model

Applying this logic to build a model of infectious disease

Let’s start with some history

In 1926-27, Volterra and Lotka developed the model of consumer–resource dynamics

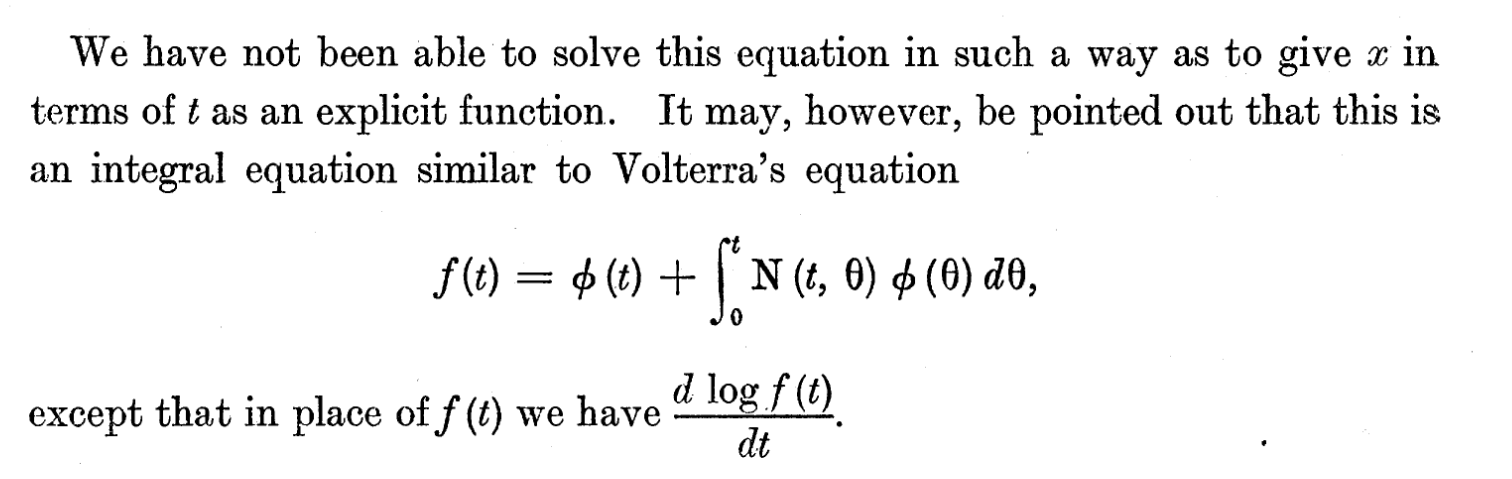
Kermack and McKendrick’s model

Assumptions

  • In our focal population, individuals are either \(S\)usceptible to a given disease, are currently \(I\)nfected with the disease, or have recently \(R\)ecovered from the disease.
    • (The model is often called the \(SIR\) model for this reason)
  • \(S\)usceptible individuals get infected at a rate \(\beta\) when the encounter individuals that are currently \(I\)nfected
  • \(I\)nfected individuals recover from infection at a rate \(\gamma\)
    • This is equivalent to saying that infected individuals stay infected for \(\frac{1}{\gamma}\) amount of time
  • \(R\)ecovered individuals have immunity from the disease for life
  • This could make sense for a non-fatal disease that moves through quickly
  • E.g. the disease moves quickly enough that we don’t need to think about any births happening in the population
  • We can modify the model for diseases that behave differently (e.g. what if recovered individuals lose their immunity over some period of time?) . . .

flowchart LR
  Susceptible --> Infected --> Recovered

Assumptions

  • In our focal population, individuals are either \(S\)usceptible to a given disease, are currently \(I\)nfected with the disease, or have recently \(R\)ecovered from the disease.
    • (The model is often called the \(SIR\) model for this reason)
  • \(S\)usceptible individuals get infected at a rate \(\beta\) when the encounter individuals that are currently \(I\)nfected
  • \(I\)nfected individuals recover from infection at a rate \(\gamma\)
    • This is equivalent to saying that infected individuals stay infected for \(\frac{1}{\gamma}\) amount of time
  • \(R\)ecovered individuals have immunity from the disease for life

To model this system we need three equations: \(\frac{dS}{dt}\), \(\frac{dI}{dt}\), \(\frac{dR}{dt}\)

\[\frac{dS}{dt} = -\beta SI\]

\[\frac{dI}{dt} = \beta SI - \gamma I\]

\[\frac{dR}{dt} = \gamma I\]

What do we expect to happen in this system?

\[\frac{dS}{dt} = -\beta SI\]

\[\frac{dI}{dt} = \beta SI - \gamma I\]

\[\frac{dR}{dt} = \gamma I\]

  • The number of susceptible individuals is always declining
  • Eventually, every individual will get infected, and will eventually recover
  • At equilibrium, all individuals will be in the Recovered category

What if the system is more complicated?

  • E.g. individuals lose immunity over time

flowchart LR
  Susceptible --> Infected --> Recovered
  Recovered --> Susceptible

  • E.g. what if there is a vaccine that allows people to gain immunity without becoming infected?

flowchart LR
  Susceptible --> Infected --> Recovered
  Susceptible --> Vaccinated

  • E.g. what if the disease is fatal, such that not all infected individuals recover?

flowchart LR
  Susceptible --> Infected --> Recovered
  Infected --> Dead

  • Some disease move through populations slowly enough that vital rates (birth and daeth rates) become important

    • Are newborns susceptible or immune (innate/maternal immunity)?

  • Some diseases exist in which there are individuals who are carriers but not infected. These carriers don’t get sick but can get others sick.

  • Some diseases have an ‘Incubation’ period after infection (i.e. infected individual doesn’t immediately show signs of infection)

  • Stage/age structure: some diseases cause more effects in older or younger patients – combining matrix model approaches with SIR approach

Next class

  • Some lessons from compartment models for understanding disease dynamics

Ecology of infectious diseases

Consider a simple model of disease dynamics (“SIR”)

flowchart LR
  Susceptible --> Infected --> Recovered

  • Rate of transmission: \(\beta\)
  • Rate of recovery: \(\gamma\)
  • Consider a “closed” population: infection is rapid-acting, so births and deaths are not relevant for now.
  • For simplicity, define \(S, I, R\) as the proportion of individuals in each compartment

\(S = \frac{\text{total susceptible}}{\text{total number of individuals}}\),

\(I = \frac{\text{total infected}}{\text{total number of individuals}}\)

\(R = \frac{\text{total recovered}}{\text{total number of individuals}}\)

flowchart LR
  Susceptible --> Infected --> Recovered

\[\frac{dS}{dt} = -\beta SI\]

\[\frac{dI}{dt} = \beta SI - \gamma I\]

\[\frac{dR}{dt} = \gamma I\]

Insights from the SIR model

In infectious disease modeling, an important question is:

Under what conditions would a new disease spread through a population?

  • Consider a population that has never before encountered a particular disease
  • There is no innate immunity, so all individuals are currently in the \(S\)usceptible compartment (\(S = N\))
  • One individual gets infected (\(I = 1\), \(S = (N-1)\))
    • “Patient zero”
  • Will the disease spread, or will it be contained to just Patient Zero?
  • In other words: will \(I\) grow or shrink?
    • \(\frac{dI}{dt} > 0\)

Insights from the SIR model

To know whether an infection will spread, we need to know whether the following is true:

\[\frac{dI}{dt} = \beta SI - \gamma I \gt 0\]

  • If true, infection spreads
  • If not true, the infection should disappear over some time

What needs to be true for

\[\frac{dI}{dt} = \beta SI - \gamma I \gt 0\]

\[\beta SI - \gamma I \gt 0\]

\[\beta SI \gt \gamma I\]

\[\beta S \gt \gamma \]

  • In this population, most individuals are susceptible (only 1 is infected)
  • We defined \(S\) as the proportion of individuals that are susceptible – nearly everyone is!
    • So, \(S \approx 1\)

\[\frac{\beta}{\gamma} > 1 ~~~\text{for}~~~ \frac{dI}{dt} > 0\]

\[\frac{\beta}{\gamma} > 1 ~~~\text{for}~~~ \frac{dI}{dt} > 0\]

On the other hand, for the disease to not spread,

\[\frac{\beta}{\gamma} < 1 ~~~\text{for}~~~ \frac{dI}{dt} < 0\]

We give this number a special name:

\[\overbrace{R_0}^{\substack{\text{basic} \\ \text{reproductive} \\ \text{rate}}} = \frac{\beta}{\gamma}\]

  • Number of new infections per infector in a population

What controls \(R_0\)

\[R_0 = \frac{\beta}{\gamma}\]

  • \(R_0 > 1\) implies an infection can spread; \(R_0<1\) implies an infection cannot spread

  • \(R_0\) can change over time (e.g. because of change virulence of the disease or change in behavior), so we can focus on \(R_{0,t}\) (\(R_0\) at a given time \(t\))

  • When is \(R_{0, t}\) big?

  • What can we do to reduce \(R_{0, t}\)?

    • Decrease \(\beta\)
    • Increase \(\gamma\)

\(R_{0,t}\) is used by public health agencies to monitor trends:

https://www.cdc.gov/cfa-modeling-and-forecasting/rt-estimates/index.html

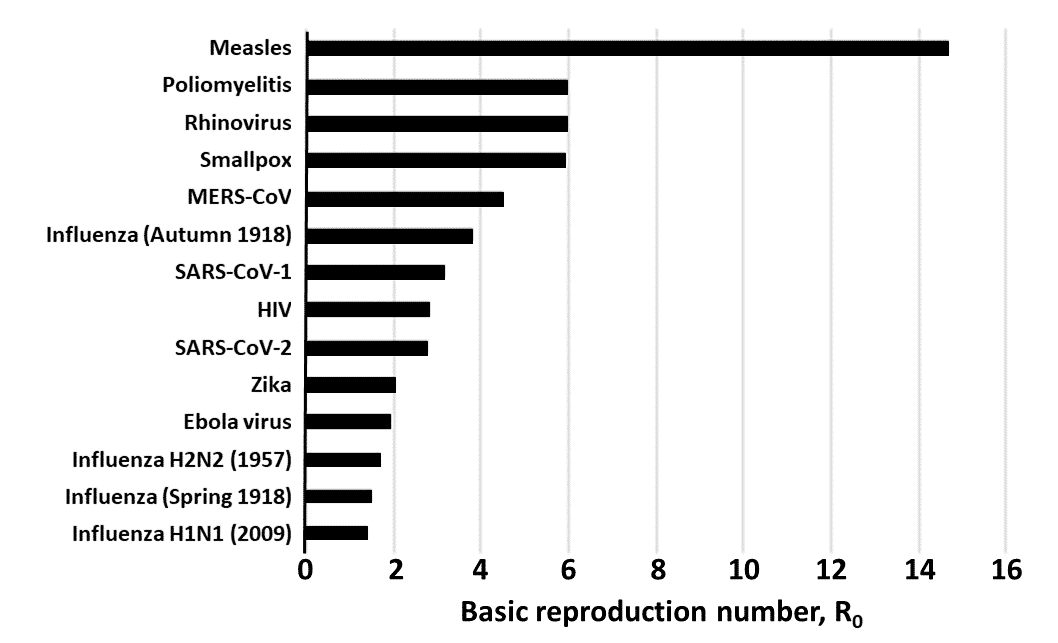
\(R_0\) for important infections, from the Center for Evidence Based Medicine, Oxford Univ.

Infectious disease ecology wrapup

\[\frac{dS}{dt} = -\beta SI\]

\[\frac{dI}{dt} = \beta SI - \gamma I\]

\[\frac{dR}{dt} = \gamma I\]

  • If a new disease emerges, will it spread or not?

\[\frac{dI}{dt} = \beta SI - \gamma I\]

  • When is this above zero?

\[\beta SI > \gamma I\]

\[\beta S > \gamma\]

  • When a disease first emerges, almost everyone will be susceptible to it: \(S \approx 1\)

\(\beta > \gamma\), which is the same as \(\frac{\beta}{\gamma} > 1\)

\[\frac{\beta}{\gamma} > 1\]

  • We give the ratio \(\frac{\beta}{\gamma}\) a special name: \(R_0\) (“R-naught”) or basic reproductive rate of the disease

  • If \(R_0>1\), the disease is predicted to spread after it first enters the system; otherwise, it cannot spread.

  • Recall that the assumption behind \(R_0\)’s equation is that we are thinking about the disease immediately after it enters the population, so \(S \approx 1\)

    • But as a disease circulates through a population, this will change – many individuals will be infected and (hopefully) recovered

  • So in real life, disease ecologists track \(R_t\), or disease reproductive rate at a given time.

\[R_0 = \frac{\beta}{\gamma}\]

  • Reducing \(R_0\) requires either reducing \(\beta\) or increasing \(\gamma\)

  • \(\beta\) is the transmission probability if an interaction does happen – can be hard to modify

  • \(\gamma\) is the recovery rate of infected individuals – can be hard to lower for brand new infections

  • Over time, these numbers can change, e.g. due to evolution of the infectious disease itself or due to better recovery

  • But at the time of disease introduction, these can be hard

Reducing disease spread without altering \(R_0\)

  • Reducing \(R_0\) requires reducing \(\beta\), but if we can’t, the next best thing is to have fewer interactions between Susceptible and Infectious individuals:

\[\frac{dS}{dt} = -\beta SI\]

\[\frac{dI}{dt} = \beta SI - \gamma I\]

\[\frac{dR}{dt} = \gamma I\]

Fewer interactions requires measures like quarntining, or moving individuals out of the \(S\)uscptible category – which is possible through vaccination.

Other resources for learning about applications of SIR models: