Week 10
Quantifying biodiversity

Recap from last week

Reductionist and holistic approaches

So far, we have taken a reductionist approaches to study ecological process:

  • Study a complex system by breaking it down into component interactions

    • e.g. In a forest that houses hundreds of tree species, how do two interact with each other?

We contrasted this with a “holistic” approach

  • Study complex systems as whole systems

  • Emphasis on “Emergent properties” that are only evident when we study the full system

Reductionist and holistic approaches

Using a reductionist approach, we have focused on mechanisms that explain why nature is the way it is

  • E.g. “Why can species coexist in some conditions but not other?”

We will now study similar patterns but at a higher scale

  • Goal is to identify what patterns do exist,

  • and why they come to be.

  • e.g. Is there more biodiversity in some parts of the Earth than others? Why?

  • e.g. Within Louisiana, are there times of the year where natural communities have more biodiversity than others? Why?

Over the next few weeks, we will over a range of scales

  • Small-ish spatial scales, e.g. patterns of diversity across a single mountain

  • Medium spatial scales, e.g. differences in biodiversity across islands in an archipelago

  • Large spatial scales, e.g. continental patterns

  • We will also explore variation in biodiversity across temporal scales (i.e. change over time)

Let’s start with a simple question

In Week 1, we asked a simple question: How many bats live under a bridge in Austin?

We will now ask a second simple question: What is the biodiversity of an ecological community?

  • Case study: birds in Baton Rouge

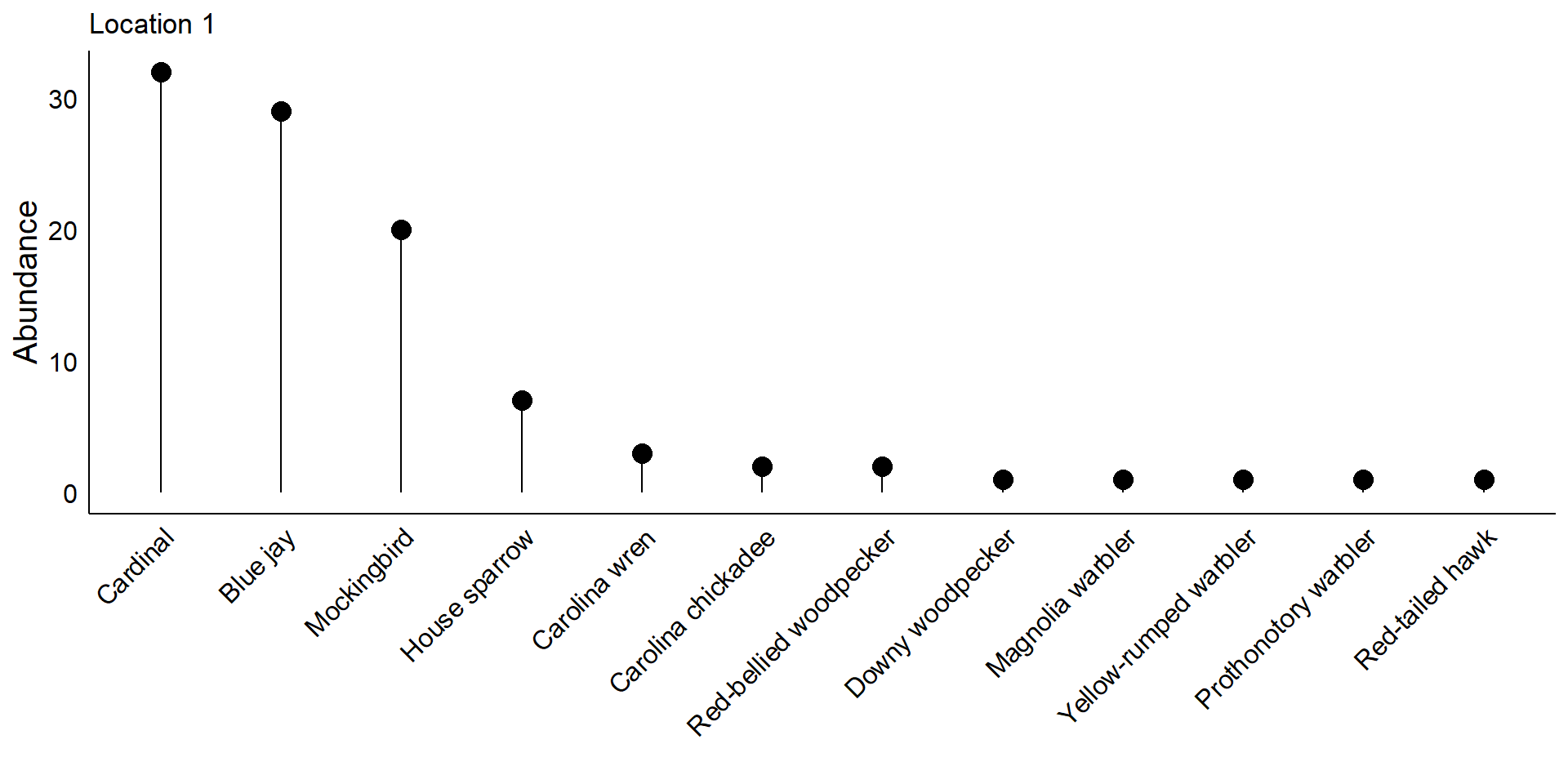
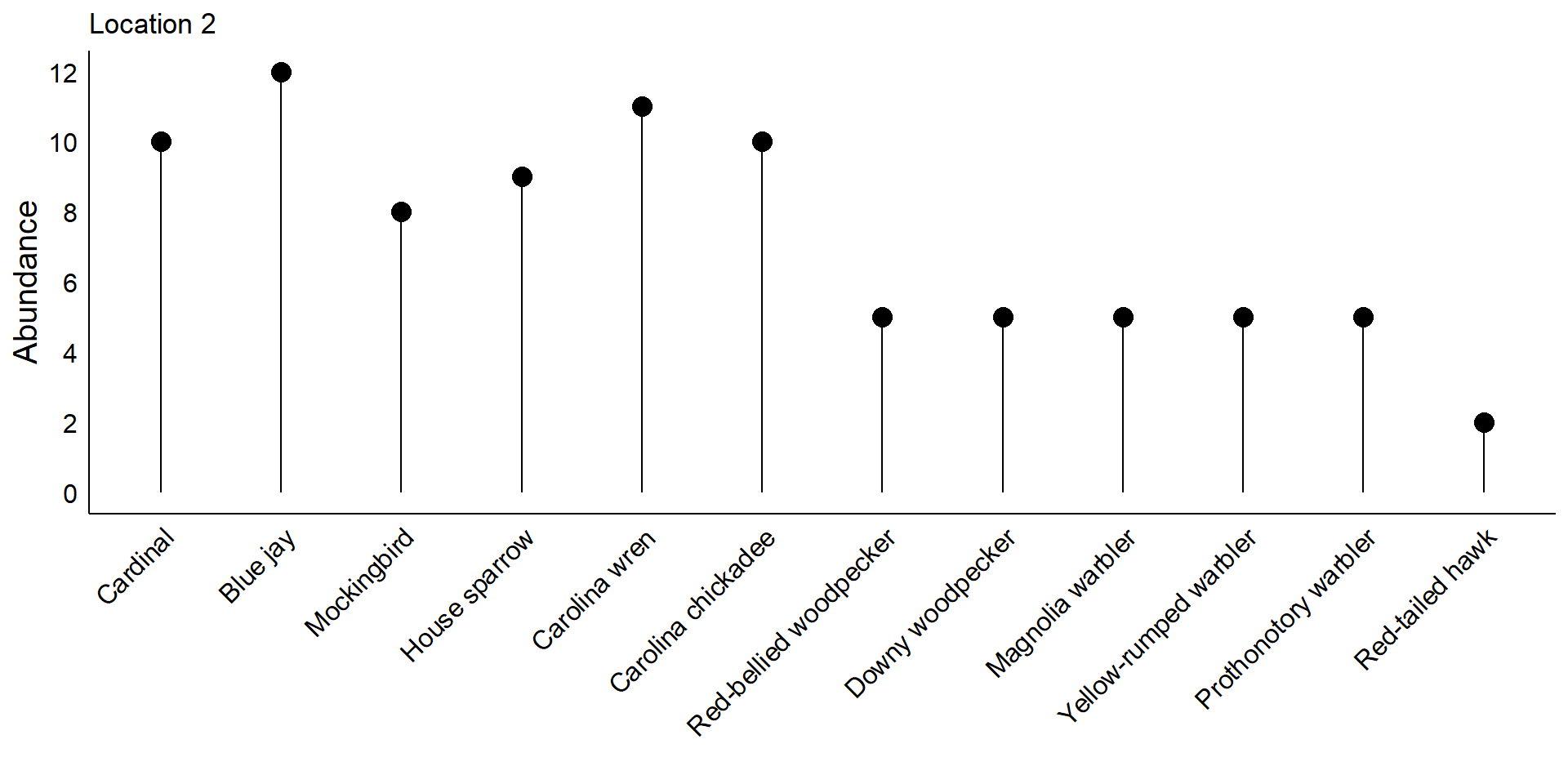
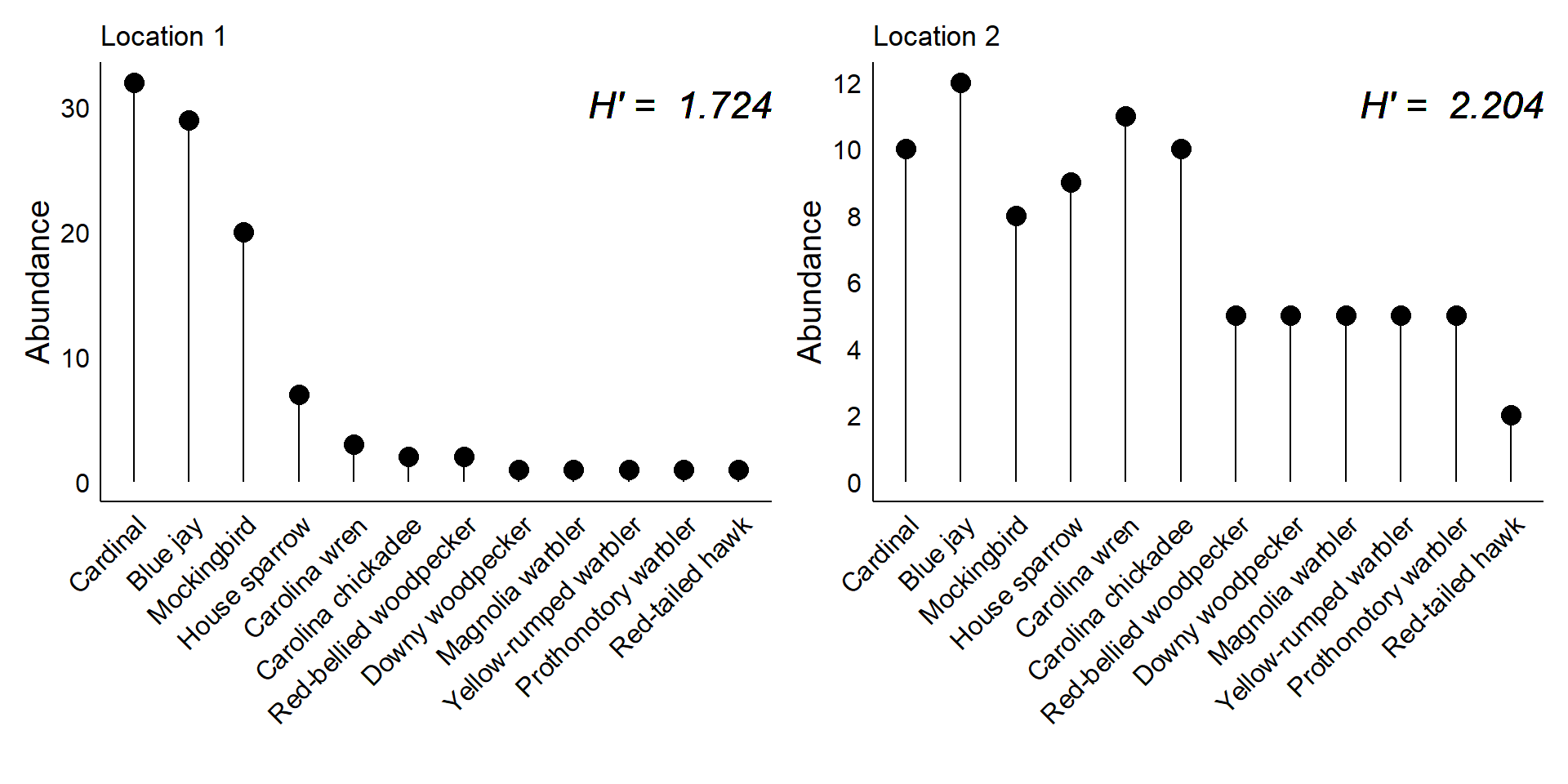
Some common birds of Baton Rouge

Cardinal

Blue Jay

Mockingbird

House sparrow

Carolina wren

Carolina chickadee

Red-bellied woodpecker

Downy woodpecker

Magnolia warbler

Yellow-rumped warbler

Prothonotory warbler

Red tailed hawk

Consider two locations where the same set of twelves species can be found.

In the first location, the bird community is dominated by just a few species:

In second location, individuals from each species are fairly common:

Small group discussion:

  • What is the biodiversity in each location?

  • If you go to Location 1 vs. Location 2 and spend 10 minutes in each, do you think you would see an equal number of species?

Other dimensions of biodiversity

Community 1

Red-bellied woodpecker

Downy woodpecker

Pileated woodpecker

Yellow-bellied sapsucker

Community 2

Red-bellied woodpecker

Prothonotory warbler

Red tailed hawk

Carolina chickadee

Other dimensions of biodiversity

  • Communities can have different amount of “Phylogenetic history” represented in their species list

Quantifying biodiversity…

… isn’t so simple either.

  • How to account for variation in abundance?

  • How to acccount for variation in functional differences?

  • How to account for phylogenetic history differences?

We need to use some clever math to help us quantify these patterns!

Accounting for variation in abundance

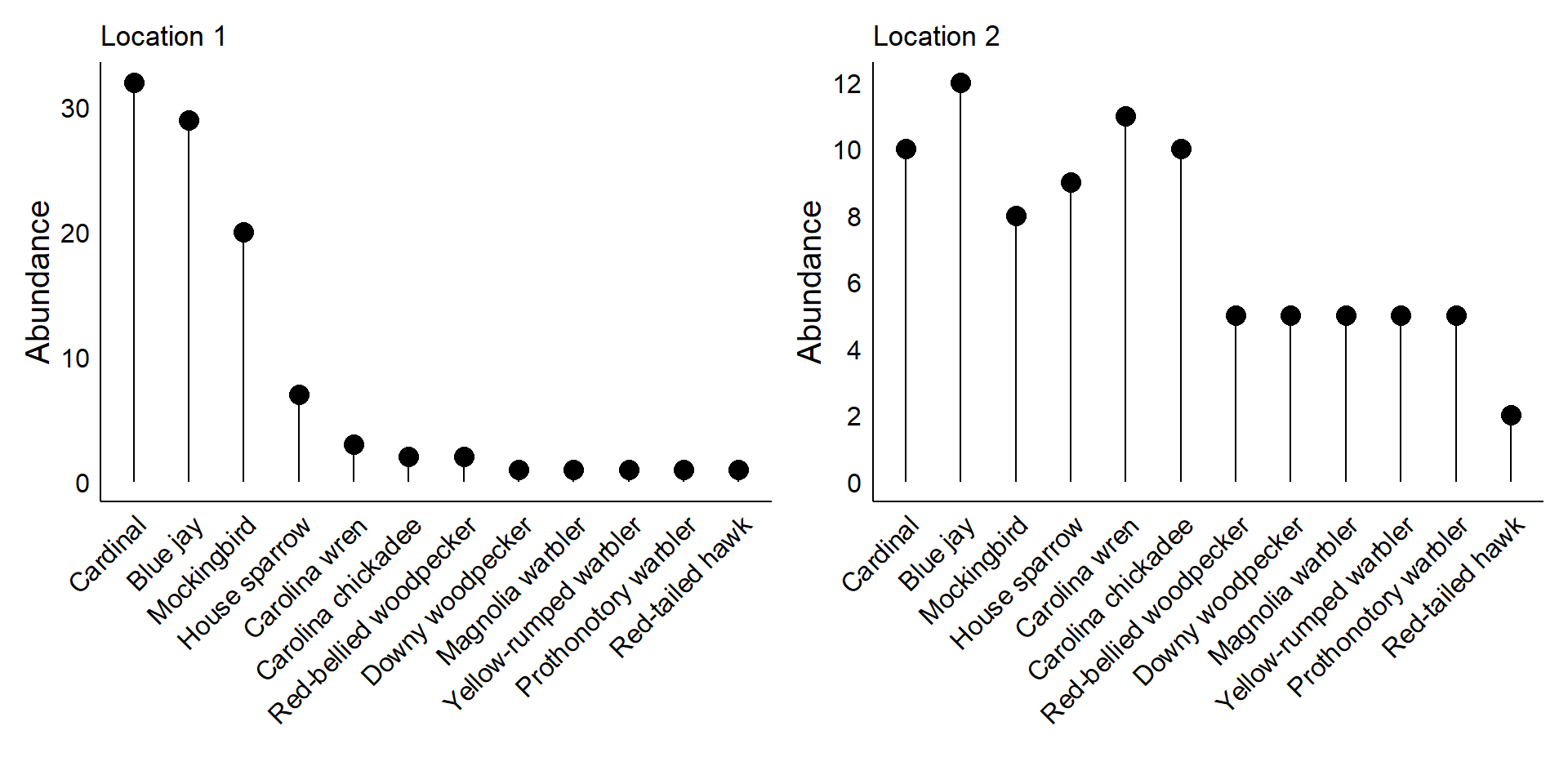
  • If I were randomly finding birds in Location 1 and had to guess which species I would find next, which should I guess?

Shannon diversity index

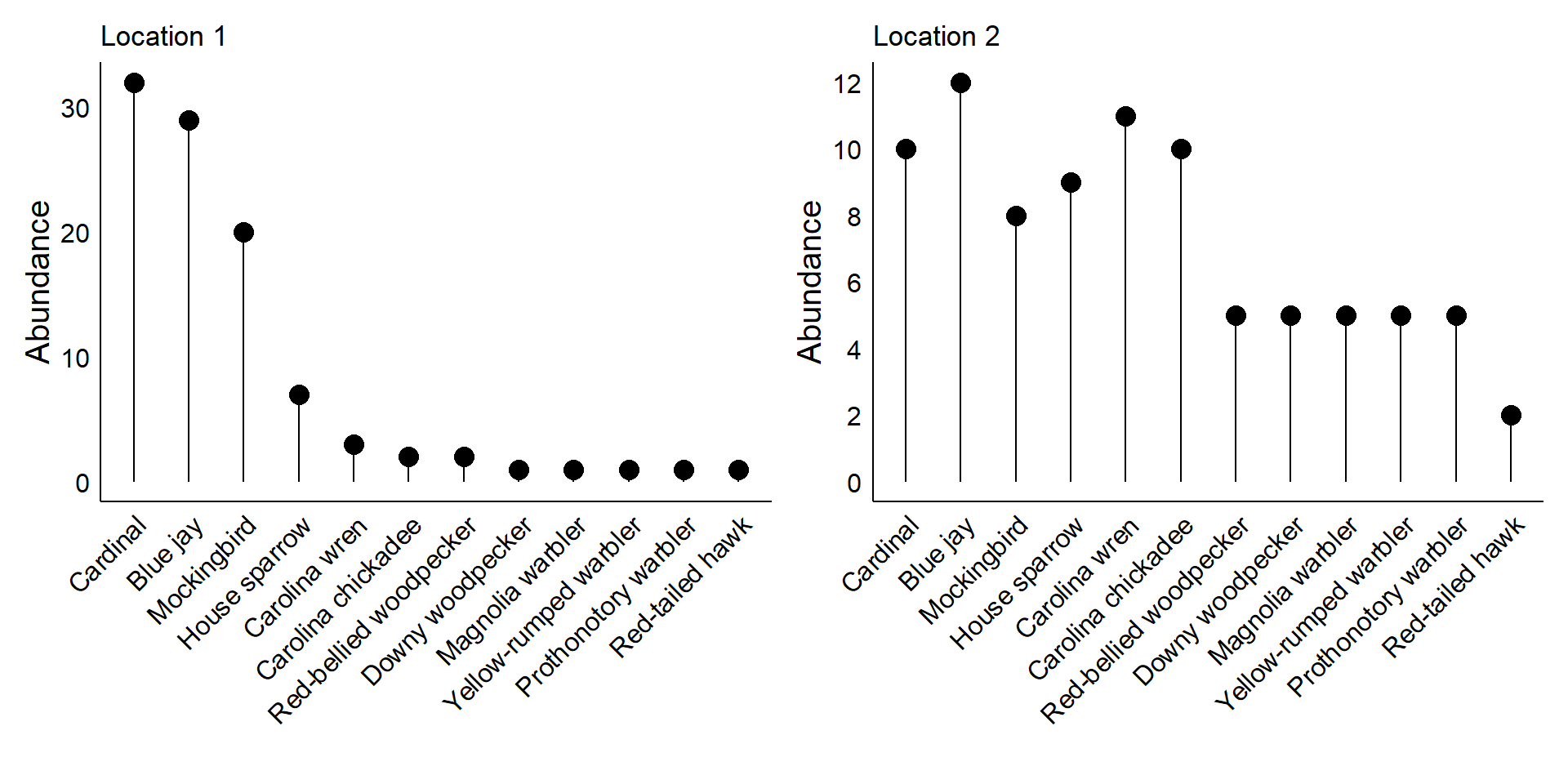
  • How about in Location 2?

Shannon diversity index

  • Location 1 is more “predictable”
  • Higher degree of “surprise” in Location 2
  • This is also called “Information entropy”
  • Commonly used across science, e.g. in computers, to optimize information storage and transfer

Shannon diversity index

A quantitative measure of biodiversity and community “evenness”

\[\overbrace{H'}^{\substack{\text{Shannon}\\{\text{index}}}} = -\sum_{i = 1}^{n} \overbrace{p_i}^{\substack{\text{proportional}\\ \text{abundance}}}*\overbrace{\text{ ln}(p_i)}^{\log\big(\substack{\text{proportional}\\ \text{abundance}}\big)}\]

Calculating Shannon diversity

species Abundance proportion log(proportion) contribution
Cardinal 32
Blue jay 29
Mockingbird 20
House sparrow 7
Carolina wren 3
Carolina chickadee 2
Red-bellied woodpecker 2
Downy woodpecker 1
Magnolia warbler 1
Yellow-rumped warbler 1
Prothonotory warbler 1
Red-tailed hawk 1

Calculating Shannon diversity

species Abundance proportion log(proportion) contribution
Cardinal 32 0.32
Blue jay 29 0.29
Mockingbird 20 0.20
House sparrow 7 0.07
Carolina wren 3 0.03
Carolina chickadee 2 0.02
Red-bellied woodpecker 2 0.02
Downy woodpecker 1 0.01
Magnolia warbler 1 0.01
Yellow-rumped warbler 1 0.01
Prothonotory warbler 1 0.01
Red-tailed hawk 1 0.01

Calculating Shannon diversity

species Abundance proportion log(proportion) contribution
Cardinal 32 0.32 -1.139
Blue jay 29 0.29 -1.238
Mockingbird 20 0.20 -1.609
House sparrow 7 0.07 -2.659
Carolina wren 3 0.03 -3.507
Carolina chickadee 2 0.02 -3.912
Red-bellied woodpecker 2 0.02 -3.912
Downy woodpecker 1 0.01 -4.605
Magnolia warbler 1 0.01 -4.605
Yellow-rumped warbler 1 0.01 -4.605
Prothonotory warbler 1 0.01 -4.605
Red-tailed hawk 1 0.01 -4.605

Calculating Shannon diversity

species Abundance proportion log(proportion) contribution
Cardinal 32 0.32 -1.139 -0.364
Blue jay 29 0.29 -1.238 -0.359
Mockingbird 20 0.20 -1.609 -0.322
House sparrow 7 0.07 -2.659 -0.186
Carolina wren 3 0.03 -3.507 -0.105
Carolina chickadee 2 0.02 -3.912 -0.078
Red-bellied woodpecker 2 0.02 -3.912 -0.078
Downy woodpecker 1 0.01 -4.605 -0.046
Magnolia warbler 1 0.01 -4.605 -0.046
Yellow-rumped warbler 1 0.01 -4.605 -0.046
Prothonotory warbler 1 0.01 -4.605 -0.046
Red-tailed hawk 1 0.01 -4.605 -0.046

Measuring diversity & patterns of biodiversity

University Lakes bird biodiversity

Data from 2023

University Lakes bird biodiversity

Data from 2024

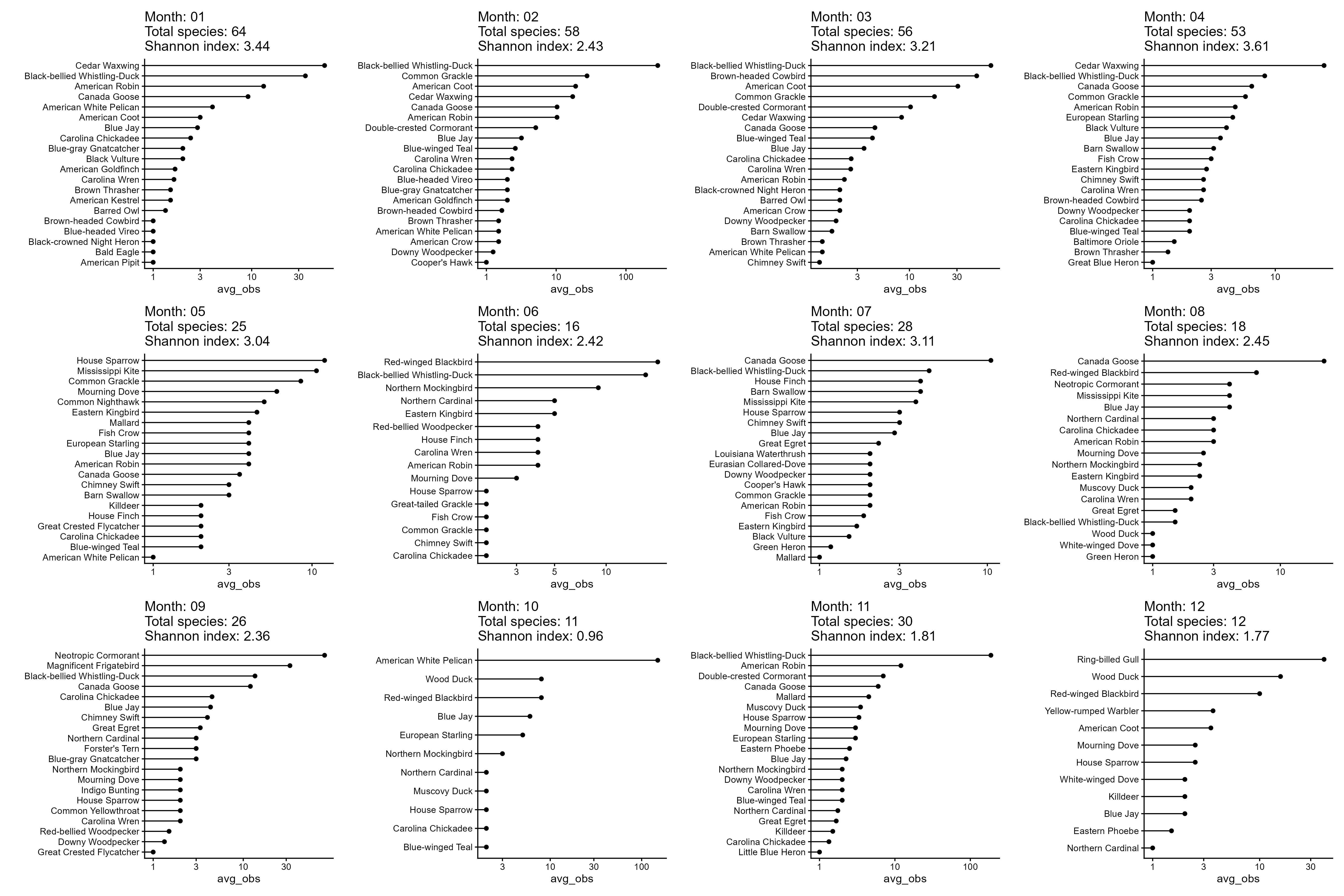
Shannon diversity: a measure of “surprise”

Biodiversity is variable

  • Across time (e.g. More diversity in some seasons than other; More diversity in some years than others; More biodiversity in some time periods than others)

  • Across space (e.g. More diversity in one part of Baton Rouge than another; More diversity in some parts of Louisiana than other; More biodiversity in some parts of the globe than other)

  • But it is not just the number of species that are variable; we can also need to think about heterogeneity across time and space

Example 1

Consider a landscape that comprises several different habitat patches.

  • Each habitat patch has a given number of species

  • How much total diversity is there in the whole landscape?

Example 2

Consider a different landscape that comprises several different habitat patches.

  • Each habitat patch has a given number of species

  • How much total diversity is there in the whole landscape?

Measuring biodiversity at scale

  • Requires knowledge of who lives where, and when

  • Requires metrics that capture not just numbers of species, but changes in species identity

The geographic scales of biodiversity

pop quiz: how many species of native plants are in Louisiana?

“Did you know that Louisiana has about 2,500 native plants?”

But, not all plants are everywhere!

. . . Bottomland Hardwood Forests and Swamps

Prominent Physical Features: Forested wetlands that occupy broad floodplains and depressions bordering large river systems. The soil, hydrology and plant community vary based on river influence and landscape position. Floodplain soils are fertile and desired for agriculture, so most of the original forests have been converted to agriculture. Flood control efforts have also degraded the forests of this plant region.

Prominent Vegetation: Oaks, cottonwood, sycamores, elms, maples and ashes in bottomland hardwood forests. Bald cypress, water tupelo and swamp tupelo occur in the swamps

Coastal Prairies

Prominent Physical Features: Coastal Prairies Prominent Physical Features: Extension of Midwestern tall-grass prairie, with a subtropical influence. Once covered approximately 2.5 million acres in Louisiana. Modern agriculture has reduced Louisiana’s coastal prairie to less than 1 percent of its former extent. Today, coastal prairie is limited to small remnants on grazing land, along railroads and a few small patches in urban areas. Fire, along with harsh soil conditions, restrict woody species to forests along streams dissecting the plant region

Prominent Vegetation: A diverse mix of lush grasses (little bluestem, big bluestem, eastern gamma grass, switchgrass, and Indian grass), sedges, rushes, and many wildflowers.

There is clearly lots of turnover between regions

Bottomland Hardwood Forests and Swamps

Prominent Vegetation: Oaks, cottonwood, sycamores, elms, maples and ashes in bottomland hardwood forests. Bald cypress, water tupelo and swamp tupelo occur in the swamps

Coastal Prairies

Prominent Vegetation: A diverse mix of lush grasses (little bluestem, big bluestem, eastern gamma grass, switchgrass, and Indian grass), sedges, rushes, and many wildflowers.

Such turnover can also happen on local scales

e.g. Within a forest, the plant community next to a streambed (wet soils) will be different from the plant community at the top of a ridge (dry soils)

Making sense of diversity patterns

The concepts of \(\alpha\), \(\beta\), and \(\gamma\) diversity help us make sense of these patterns.

  • Biodiversity at the largest scale: \(\gamma\) diversity.
    • e.g. 2,500 native plants in Louisiana
  • Biodiversity at the smallest scale: \(\alpha\) diversity.
    • e.g. 200 species of grasses and wildflowers at a Coastal Prairie south of Lafayette
  • Biodiversity turnover (differences) between local ares: \(\beta\) diversity
    • e.g. There are 200 species in a Louisiana Coastal Prairie and 150 species in a Longleaf Pine Savanna, but 50 of the species are unique to prairie, and 100 of the species are unique to longleaf pine.

Biodiversity patterns in action

In the following communities, each species is represented by a different letter.

Let’s calculate \(\alpha\), \(\beta\), and \(\gamma\) diversity.

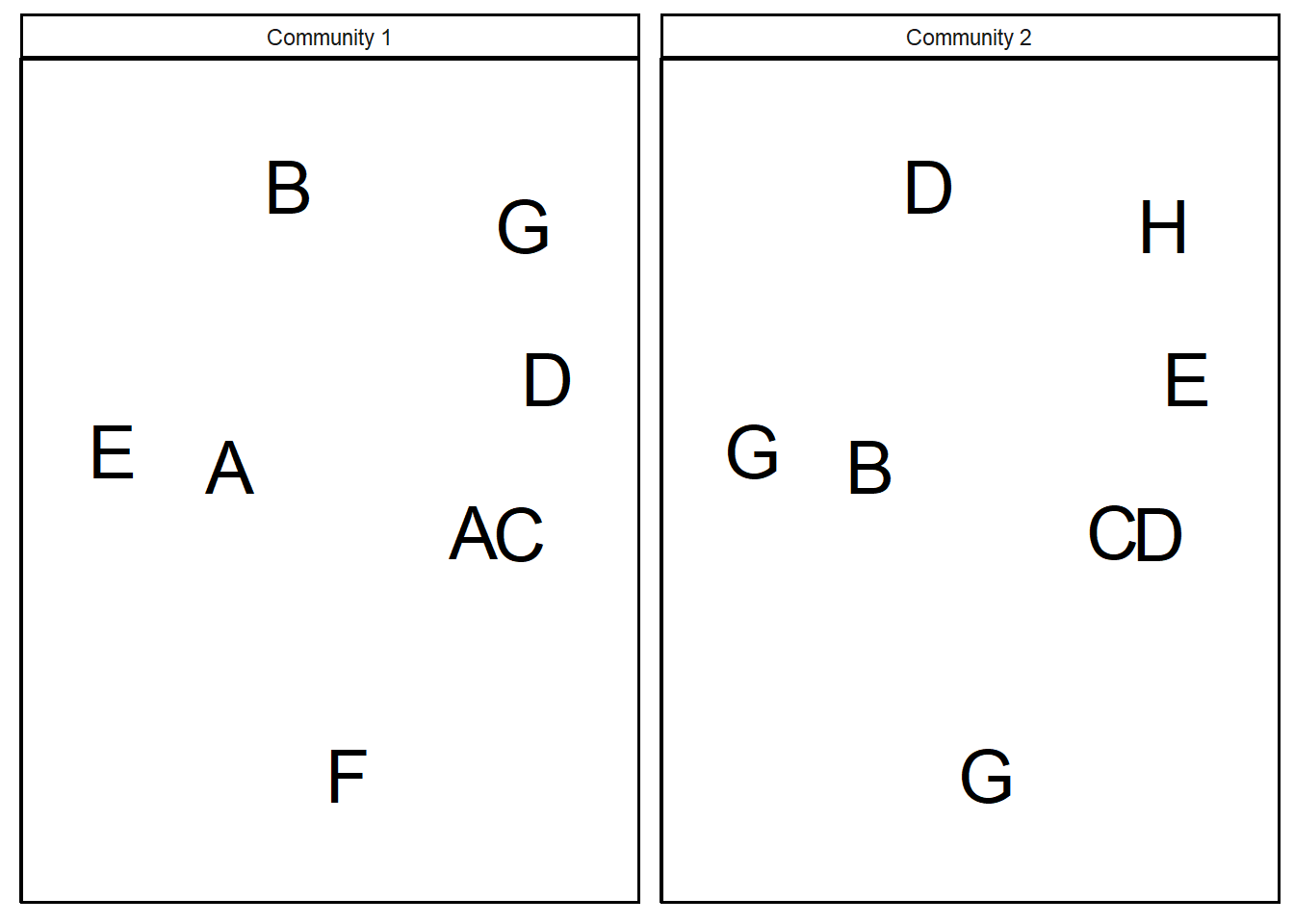
  • \(\alpha_{\text{community }1} = 7 \text{ species}\)

  • \(\alpha_{\text{community }2} = 6 \text{ species}\)

  • \(\gamma = 8 \text{ species}\) (A,B,C,D,E,F,G,H)

  • \(\beta\) is the number of species unique to one community

    • Species \(A\) and \(F\) only in Community 1
    • Species \(H\) only in Community 2
    • \(\beta = 3\) unique species

Your turn: calculate \(\alpha\), \(\beta\), and \(\gamma\) diversity for the following

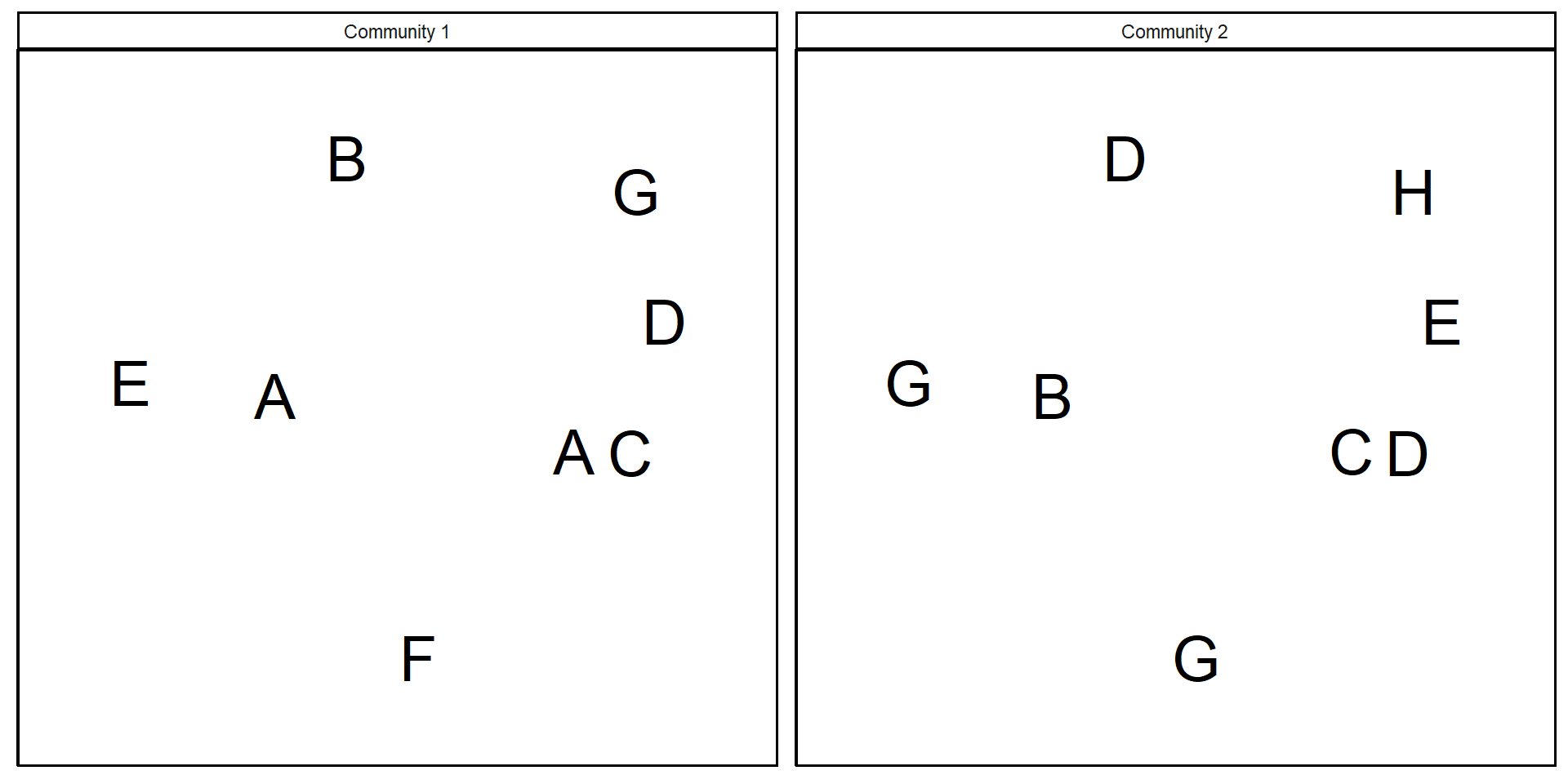
  • Here, we are introducing \(\beta\) diversity over space – but we can also think about \(\beta\) diversity over time

  • How many (and which) species are found in University Lakes in January? How about in March?

  • \(\beta\) diversity is an important and complicated concept

Why bother?!

  • \(\beta\)-diversity is fundamentally an attempt to quantify changes in diversity
  • Originally, the concept was developed to understand patterns of species turnover across space (e.g. from the base of a mountain to the top; from the source of a river to its mouth)
  • But it has vast implications for some of the most pressing questions today:
    • How is biodiversity different at the edge of a forest vs. in its interior?
    • How is biodiversity different near cities vs. rural vs. protected areas?
    • How is the gut microbiome of someone living in a city different from a person living rurally?

Why bother?!

  • \(\beta\)-diversity is fundamentally an attempt to quantify changes in diversity
  • Originally, the concept was developed to understand patterns of species turnover across space
  • But we can adapt it to ask questions about change in biodiversity over time
    • How did biodiversity in the Gulf of Mexico change before/after the oil spill?
    • How does the pollinator biodiversity of a neighborhood change when we start planting native flowering plants?
    • How does my gut biodiversity change when I change my exercise regime?

Why bother?!

Quantifying patterns of biodiversity is essential for getting a good grasp on managing and protecting biodiversity

More on this in the next two weeks.